题目内容
若A是△ABC的一个内角，且有sin2A=
，则sinA+cosA=（ ）
| 2 |
| 3 |
分析：由条件可得sinA＞0，cosA＞0，A为锐角．再根据 （sinA+cosA）2=1+2sinAcosA的值，求得sinA+cosA的值．
解答：解：由于A是△ABC的一个内角，且有sin2A=
=2sinAcosA，
∴sinA＞0，cosA＞0，A为锐角．
再根据 （sinA+cosA）2=1+2sinAcosA=
，则sinA+cosA=
，
故选A．
| 2 |
| 3 |
∴sinA＞0，cosA＞0，A为锐角．
再根据 （sinA+cosA）2=1+2sinAcosA=
| 5 |
| 3 |
| ||
| 3 |
故选A．
点评：本题主要考查同角三角函数的基本关系的应用，二倍角公式的应用，属于中档题．
练习册系列答案
相关题目
若A是△ABC的一个内角，且sinA+cosA=
，△ABC的形状是（ ）
| 2 |
| 3 |
| A、锐角三角形 | B、直角三角形 |
| C、钝角三角形 | D、不确定 |
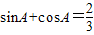，△ABC的形状是（ ）
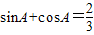，△ABC的形状是（ ）