题目内容
若A是△ABC的一个内角，且sinA+cosA=
，△ABC的形状是（ ）
| 2 |
| 3 |
| A、锐角三角形 | B、直角三角形 |
| C、钝角三角形 | D、不确定 |
分析：根据sinA+cosA=
sin(A+
)=
＜1，可知A为钝角．
| 2 |
| π |
| 4 |
| 2 |
| 3 |
解答：解：∵sinA+cosA=
sin(A+
)=
＜1，
∴A为钝角∴为△ABC钝角三角形
故选C．
| 2 |
| π |
| 4 |
| 2 |
| 3 |
∴A为钝角∴为△ABC钝角三角形
故选C．
点评：在三角形中考查三角函数取值范围，是常考内容．
练习册系列答案
阅读快车系列答案
相关题目
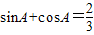，△ABC的形状是（ ）
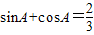，△ABC的形状是（ ）