Question

（09年潍坊一模文）(12分)

    已知双曲线的左、右两个焦点为, ，动点P满足|P|+| P |=4.

    (I)求动点P的轨迹E的方程；

    (1I)设过且不垂直于坐标轴的动直线l交轨迹E于A、B两点，问：终段O

上是否存在一点D，使得以DA、DB为邻边的平行四边形为菱形?作出判断并证明.

Answer 1

解析：（Ⅰ）双曲线的方程可化为          …………1分

    ,

    ∴P点的轨迹E是以为焦点，长轴为4的椭圆            …………2分

设E的方程为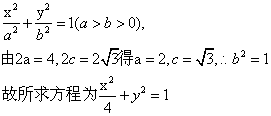          …………4分

（Ⅱ）满足条件的D                                           …………5分

    设满足条件的点D（m,0）,则

    设l的方程为y=k(x-)(k≠0),

    代人椭圆方程，得           …………6分

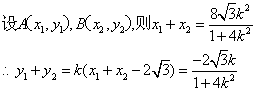
∵以DA、DB为邻边的平行四边形为菱形，

                                             …………6分

∴存在满足条件点D                                             …………12分