题目内容
设函数 中,
中, 为奇数,
为奇数, 均为整数,且
均为整数,且 均为奇数.求证:
均为奇数.求证: 无整数根。
无整数根。
详见解析.
解析试题分析:采用反证法,假设 有整数根
有整数根 ,则
,则 ,进而
,进而 均为奇数,即
均为奇数,即 为奇数,
为奇数, 为偶数,即可得到
为偶数,即可得到 也为奇数,即可得到
也为奇数,即可得到 为奇数,即
为奇数,即 与
与 均为奇数,这与
均为奇数,这与 ,
, 为奇数,
为奇数, 为奇数时,
为奇数时, 为偶数矛盾,故命题得证.
为偶数矛盾,故命题得证.
证明:假设 有整数根
有整数根 ,则
,则 (2分)
(2分)
而 均为奇数,即
均为奇数,即 为奇数,
为奇数, 为偶数,(4分),
为偶数,(4分),
∵ 为奇数,∴
为奇数,∴ 也为奇数 (6分)
也为奇数 (6分)
∵ 为奇数,∴
为奇数,∴ 为奇数;∴
为奇数;∴ 与
与 均为奇数 (9分)
均为奇数 (9分)
∵ ,
, 为奇数,
为奇数, 为奇数,∴
为奇数,∴ 又为偶数 矛盾 (11分)
又为偶数 矛盾 (11分)
∴ 无整数根 (12分)
无整数根 (12分)
考点:函数与方程的综合运用.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
 为常数,
为常数, ,函数
,函数 ,
, 且方程
且方程 有等根.
有等根. 的解析式及值域;
的解析式及值域; ,
, ,若
,若 ,求实数
,求实数 的取值范围;
的取值范围;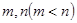 ,使
,使 的定义域和值域分别为
的定义域和值域分别为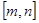 和
和 ?若存在,求出
?若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由.
 .
. 时函数
时函数 取得极小值,求a的值;(2)求函数
取得极小值,求a的值;(2)求函数
 .
. 的奇偶性;
的奇偶性; 上为减函数,求
上为减函数,求 的取值范围.
的取值范围. (
( ).
). 的定义域和值域均是
的定义域和值域均是 ,求实数
,求实数 的值;
的值; 上是减函数,且对任意的
上是减函数,且对任意的 ,
,
 ,总有
,总有 ,求实数
,求实数 ,
, .
. ,求证:函数
,求证:函数 是
是 上的奇函数;
上的奇函数; 上没有零点,求实数
上没有零点,求实数 的取值范围.
的取值范围.