题目内容
14.设集合$D=\left\{{(x,y)\left|{\left\{\begin{array}{l}x+y≥1\\ x-y≤1.\end{array}\right.}\right.}\right\}$,则下列命题中正确的是( )| A. | ?(x,y)∈D,x-2y≤0 | B. | ?(x,y)∈D,x+2y≥-2 | C. | ?(x,y)∈D,x≥2 | D. | ?(x,y)∈D,y≤-1 |
分析 作出不等式组对应的平面区域,利用二元一次不等式组表示平面区域的性质分别进行判断即可.
解答 解:集合对应的平面区域如图:
由图象知对应的区域在x+2y=-2的上方,y=-1的上方,
x-2y=0的上方和下方都有,x=2的左右都有,
故满足条件的是x+2y≥-2,
故选:B
点评 本题主要考查线性规划的应用,利用数形结合是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.已知α为第二象限角,sinα=$\frac{2\sqrt{5}}{5}$,则tan($α+\frac{π}{4}$)=( )
| A. | -3 | B. | -1 | C. | -$\frac{1}{3}$ | D. | 1 |
19.复数$\frac{\sqrt{2}+i}{1-\sqrt{2}i}$=( )
| A. | 2($\sqrt{2}$+i) | B. | 1+i | C. | i | D. | -i |
6.设实数x,y满足$\left\{\begin{array}{l}y≤2x+2\\ x+y-2≥0\\ x≤2\end{array}\right.$,则$\frac{y-1}{x+3}$的取值范围是( )
| A. | $(-∞,-\frac{1}{5}]∪[1,+∞)$ | B. | $[\frac{1}{3},1]$ | C. | $[-\frac{1}{5},\frac{1}{3}]$ | D. | $[-\frac{1}{5},1]$ |
 中,
中,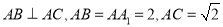 ,过
,过 的中点
的中点 作平面
作平面 的垂线,交平面
的垂线,交平面 于
于 ,则
,则 与平面
与平面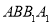 所成角的正切值为( )
所成角的正切值为( )
 B.
B.
 D.
D.
 的前
的前 项和为
项和为 ,且
,且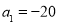 .在区间
.在区间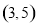 内任取一个实数作为数列
内任取一个实数作为数列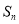 的最小值仅为
的最小值仅为 的概率为( )
的概率为( ) B.
B.
 D.
D.
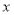 与生产总成本
与生产总成本 (万元)之间有函数关系
(万元)之间有函数关系 ,若每件产品成本平均不超过7万元,且每件产品用料6吨.现有库存原料30吨,旺季可进料900吨,旺季最高产量是( )
,若每件产品成本平均不超过7万元,且每件产品用料6吨.现有库存原料30吨,旺季可进料900吨,旺季最高产量是( )