题目内容
已知椭圆C的焦点是 、
、 ,点F1到相应的准线的距离为
,点F1到相应的准线的距离为 ,过点F2且倾斜角为锐角的直线?与椭圆C交于A、B两点,使|F2B|=3F2A|.
,过点F2且倾斜角为锐角的直线?与椭圆C交于A、B两点,使|F2B|=3F2A|.(1)求椭圆C的方程;
(2)求直线?的方程.
【答案】分析:(1)设出椭圆的方程,利用已知条件直接求出椭圆C的方程;
(2)通过焦半径,以及|F2B|=3|F2A|.求出B的坐标,然后求直线?的方程.
解答:解:(1)设椭圆C的方程为 ,
,
则由已知得:
∴b2=1,a2=b2+c2=4
∴ 为所求.
为所求.
(2)由椭圆方程知: ,设A(x1,y1),B(x2,y2)
,设A(x1,y1),B(x2,y2)
则 ,
,
 ,
,
由3|AF2|=|BF2|
得 ,
,
∴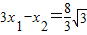 ①
①
又F2分 所成的比λ=3
所成的比λ=3
∴ ,即
,即 ②
②
由①,②得: ,
, ,
,
∴
∴
即 .
.
点评:本题考查椭圆方程的求法,焦半径公式的应用,定比分点的应用,考查计算能力,转化思想.
(2)通过焦半径,以及|F2B|=3|F2A|.求出B的坐标,然后求直线?的方程.
解答:解:(1)设椭圆C的方程为
 ,
,则由已知得:

∴b2=1,a2=b2+c2=4
∴
 为所求.
为所求.(2)由椭圆方程知:
 ,设A(x1,y1),B(x2,y2)
,设A(x1,y1),B(x2,y2)则
 ,
, ,
,由3|AF2|=|BF2|
得
 ,
,∴
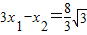 ①
①又F2分
 所成的比λ=3
所成的比λ=3∴
 ,即
,即 ②
②由①,②得:
 ,
, ,
,∴

∴

即
 .
.点评:本题考查椭圆方程的求法,焦半径公式的应用,定比分点的应用,考查计算能力,转化思想.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
 ,
, ,点P在椭圆上且满足|PF1|+|PF2|=4.
,点P在椭圆上且满足|PF1|+|PF2|=4. 的点P的个数;
的点P的个数; ,求λ2+μ2的值.
,求λ2+μ2的值.