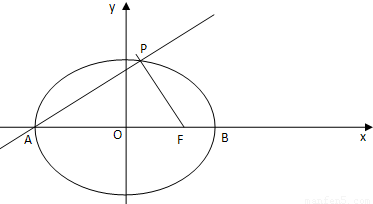
题目内容
已知椭圆C的焦点是F1( 0, -| 3 |
| 3 |
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)设直线l:2x+y+2=0与椭圆C的交点为A,B.
(i)求使△PAB的面积为
| 1 |
| 2 |
(ii)设M为椭圆上任一点,O为坐标原点,
| OM |
| OA |
| OB |
分析:(Ⅰ)待定系数法求椭圆的标准方程.
(Ⅱ)(i)把直线l方程代入椭圆的方程,求出线段AB的长度,由三角形的面积求出三角形的高是
,写出与AB平行且到AB的距离等于
直线方程,考查此直线与椭圆交点的个数.
(ii)设M(x,y),则M(x,y)满足椭圆的方程,由题中条件用点M的坐标表示出λ和μ,计算λ2+μ2的值.
(Ⅱ)(i)把直线l方程代入椭圆的方程,求出线段AB的长度,由三角形的面积求出三角形的高是
| ||
| 5 |
| ||
| 5 |
(ii)设M(x,y),则M(x,y)满足椭圆的方程,由题中条件用点M的坐标表示出λ和μ,计算λ2+μ2的值.
解答:解:(Ⅰ)∵|PF1|+|PF2|=4>|F1F2|
∴点P满足的曲线C的方程为椭圆
∵2a=4,?c=
∴b2=a2-c2=1
∴椭圆C的标准方程为x2+
=1.(4分)
(Ⅱ)(i)∵直线l:2x+y+2=0与椭圆C的交点为A,B
∴A(-1,0),?B(0,-2),|AB|=
若S△PAB=
|AB|d=
∴d=
∵原点O到直线l:2x+y+2=0的距离是
=
>
∴在直线l:2x+y+2=0的右侧有两个符合条件的P点
设直线l′:2x+y+n=0与椭圆相切,则
有且只有一个交点
∴8x2+4nx+n2-4=0有且只有一个解
由△=0解得n=2
(设负)
此时,l′与l间距离为
<
∴在直线l:2x+y+2=0的左侧不存在符合条件的P点
∴符合条件的点P有2个.(10分)
(ii)设M(x,y),则x,y满足方程:x2+
=1
∵
=λ
+μ
(λ,μ∈R)
∴(x,y)=λ(-1,0)+μ(0,-2)=(-λ,-2μ)
即:
,从而有
∴λ2+μ2=x2+
=1.(14分)
∴点P满足的曲线C的方程为椭圆
∵2a=4,?c=
| 3 |
∴b2=a2-c2=1
∴椭圆C的标准方程为x2+
| y2 |
| 4 |
(Ⅱ)(i)∵直线l:2x+y+2=0与椭圆C的交点为A,B
∴A(-1,0),?B(0,-2),|AB|=
| 5 |
若S△PAB=
| 1 |
| 2 |
| 1 |
| 2 |
∴d=
| ||
| 5 |
∵原点O到直线l:2x+y+2=0的距离是
| 2 | ||
|
2
| ||
| 5 |
| ||
| 5 |
∴在直线l:2x+y+2=0的右侧有两个符合条件的P点
设直线l′:2x+y+n=0与椭圆相切,则
|
∴8x2+4nx+n2-4=0有且只有一个解
由△=0解得n=2
| 2 |
此时,l′与l间距离为
2
| ||
|
| 1 | ||
|
∴在直线l:2x+y+2=0的左侧不存在符合条件的P点
∴符合条件的点P有2个.(10分)
(ii)设M(x,y),则x,y满足方程:x2+
| y2 |
| 4 |
∵
| OM |
| OA |
| OB |
∴(x,y)=λ(-1,0)+μ(0,-2)=(-λ,-2μ)
即:
|
|
∴λ2+μ2=x2+
| y2 |
| 4 |
点评:本题考查用待定系数法求椭圆的标准方程,点到直线的距离公式的应用,以及直线与圆锥曲线的交点问题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
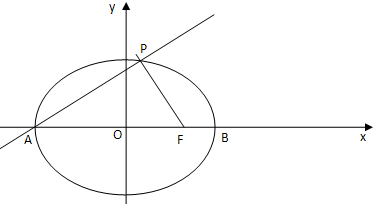 已知椭圆C的方程是
已知椭圆C的方程是 (a>b>0),点A,B分别是椭圆的长轴的左、右端点,
(a>b>0),点A,B分别是椭圆的长轴的左、右端点,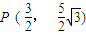 .
.