题目内容
 已知在△ABC中,∠ACB=90°,
已知在△ABC中,∠ACB=90°,(1)若BC=3,AC=4,P是AB上的点,求点P到AC,BC的距离乘积的最大值;
(2)若△ABC的面积是4,求内切圆半径的范围.
分析:(1)设P到AC,BC的距离分别为m,n,即可得到P的坐标,根据A,B的坐标求出直线AB的方程,则点P在直线AB上,代入可得m,n的关系,利用基本不等式求解即可得到答案;
(2)设BC=a,CA=b,根据题意△ABC的面积是4,可得到ab的值,利用基本不等式求出△ABC的周长的取值范围,从而运用等面积法,得到内切圆半径的取值范围.
(2)设BC=a,CA=b,根据题意△ABC的面积是4,可得到ab的值,利用基本不等式求出△ABC的周长的取值范围,从而运用等面积法,得到内切圆半径的取值范围.
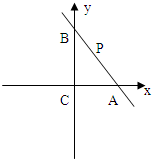
解答:解:(1)设P到AC,BC的距离分别为m,n,则P的坐标为(n,m),
∵BC=3,AC=4,
则A(4,0),B(0,3),
故由直线的截距式方程可得,直线AB的方程为
+
=1,
∵P是AB上的点,则
+
=1,
∴
+
=1≥2
,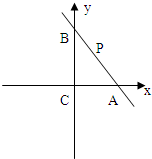
∴mn≤3,
∴点P到AC,BC的距离乘积的最大值3;
(2)设BC=a,CA=b,内切圆的半径为r,
∵△ABC的面积是4,则
ab=4,
∴ab=8,
∴△ABC的周长为BC+CA+AB=a+b+
≥2
+
=4
+4,
由三角形的“等面积法”可得,
(a+b+c)r=4,
∴r=
≤
=2
-2,
故内切圆半径的取值范围为(0,2
-2].
∵BC=3,AC=4,
则A(4,0),B(0,3),
故由直线的截距式方程可得,直线AB的方程为
| x |
| 4 |
| y |
| 3 |
∵P是AB上的点,则
| m |
| 4 |
| n |
| 3 |
∴
| m |
| 4 |
| n |
| 3 |
|

∴mn≤3,
∴点P到AC,BC的距离乘积的最大值3;
(2)设BC=a,CA=b,内切圆的半径为r,
∵△ABC的面积是4,则
| 1 |
| 2 |
∴ab=8,
∴△ABC的周长为BC+CA+AB=a+b+
| a2+b2 |
| ab |
| 2ab |
| 2 |
由三角形的“等面积法”可得,
| 1 |
| 2 |
∴r=
| 8 | ||
a+b+
|
| 8 | ||
4+4
|
| 2 |
故内切圆半径的取值范围为(0,2
| 2 |
点评:本题考查了直线的方程,基本不等式求最值,以及三角形的内切圆半径的问题.在应用基本不等式求最值时要注意“一正、二定、三相等”的判断.运用基本不等式解题的关键是寻找和为定值或者是积为定值,难点在于如何合理正确的构造出定值.第(2)问中,运用了“等面积法”求解三角形内切圆的半径是常用的方法.属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目