Question

已知函数f（x）=|x-1|+|x+1|（x∈R）
（1）证明：函数f（x）是偶函数；
（2）利用绝对值及分段函数知识，将函数解析式写成分段函数的形式，然后画出函数图象，并写出函数的值域；
（3）在同一坐标系中画出直线y=x+2，观察图象写出不等式f（x）＞x+2的解集．

Answer 1

分析：（1）根据函数的解析式，我们判断f（-x）与f（x）的关系，进而根据函数奇偶性的定义可得函数的奇偶性，
（2）先将带绝对值的函数转化成分段函数的形式，进而结合分段函数的图象和性质及偶函数图象关于y轴对称，可得函数简图；
（3）根据（2）中函数简图，数形结合可在同一坐标系中画出直线y=x+2，观察图象写出不等式f（x）＞x+2的解集．

解答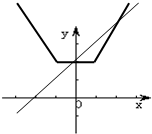：解：（1）f（-x）=|-x-1|+|-x+1|=|x+1|+|x-1|=f（x）
∴f（x）是偶函数   
（2）原函数式可化为：
f(x)=

-2x，x＜-1 2，-1≤x≤1 2x，x＞1

；其图象如图所示，
由函数图象知，函数的值域为[2，+∞）  …（9分）
（3）由函数图象知，
当x=0或2时，f（x）=x+2．
结合图象可得，不等式的解集为{x|x＜0或x＞2}…（12分）

点评：本题考查的知识点是带绝对值的函数的图象和性质，函数奇偶性的判断，其中画出函数的图象是解答本题的关键．