题目内容
有两辆汽车由南向北驶入四叉路口,各车向左转,向右转或向前行驶的概率相等,且各车的驾驶员相互不认识.(I)规定:“第一辆车向左转,第二辆车向右转”这一基本事件用“(左,右)”表示.又“(直,左)”表示的是基本事件:“第一辆车向前直行,第二车向左转”.请参照上面规定列出两辆汽车过路口的所有基本事件;
(II)求至少有一辆汽车向左转的概率;
(III)设有ξ辆汽车向左转,求ξ的分布列和数学期望.
【答案】分析:(I)每辆车在路口有三种选择,故两辆汽车过路口的所有基本事件为9种
(II)由(1)中列出的基本事件中数出至少有一辆汽车向左转的事件数,用古典概型求解即可;
(III)ξ的所有可能取值为0,1,2,分别由古典概型求概率,列出分布列,再由期望公式直接求期望即可.
解答:解:(I)(左,左);(左,直);(左,右);
(直,右);(直,左);(直,直);
(右,右);(右,直);(右,左).
基本事件共有9种
(II)至少有一辆汽车向左转的事件数有5种,所求概率P= .
.
(III)ξ的分布列为
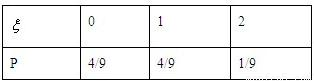
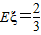 .
.
点评:本题考查古典概型、离散型随机事件的分布列、期望等知识,较简单.
(II)由(1)中列出的基本事件中数出至少有一辆汽车向左转的事件数,用古典概型求解即可;
(III)ξ的所有可能取值为0,1,2,分别由古典概型求概率,列出分布列,再由期望公式直接求期望即可.
解答:解:(I)(左,左);(左,直);(左,右);
(直,右);(直,左);(直,直);
(右,右);(右,直);(右,左).
基本事件共有9种
(II)至少有一辆汽车向左转的事件数有5种,所求概率P=
 .
.(III)ξ的分布列为

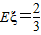 .
.点评:本题考查古典概型、离散型随机事件的分布列、期望等知识,较简单.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目