题目内容
在正北方向的一条公路上，一辆汽车由南向北行驶，速度为100 km/h，一架飞机在一定高度上的一条直线上飞行，速度为
km/h，从汽车里看飞机，在某个时刻看见飞机在正西方向，仰角为30°，在36 s后，又看见飞机在北偏西30°，仰角为30°处，问飞机的飞行高度是多少？
解:如图所示，
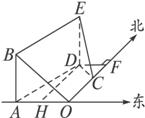
正北方向为OF，东西方向为OA，设看飞机在正西时，汽车位置是O点，飞机位置是B点，飞机正下方是A点，36 s后，汽车位置是C点，飞机位置是E点，飞机E点下方是D点，设飞机高度为x km.
∠AOB=∠ECD=∠DCF=30°
在Rt△BAO和Rt△EDC中，
OA=DC=xcot30°=
x,
BE=
×
，OC=100×
=1.
过D作DF⊥OC于F，那么
CF=CD·cos30°=
x,DF=CD·sin30°=
x.
过D作DH⊥AO于H，则HO=DF=
x，
∴AH=AO-HO=
x-
x=
x,HD=OF=OC+CF=1+
x.
∴在Rt△ADH中，AD2=AH2+DH2=
x2+(1+
x)2=3x2+3x+1
又∵AB
DE，∴BE=AD,
即7=3x2+3x+1.∴x=1
∴飞机的高度为1 km..
练习册系列答案
阅读快车系列答案
相关题目
如图，GH是东西方向的公路北侧的边缘线，某公司准备在GH上的一点B的正北方向的A处建一仓库，设AB=y km，并在公路同侧建造边长为x km的正方形无顶中转站CDEF（其中边EF在GH上），现从仓库A向GH和中转站分别修两条道路AB，AC，已知AB=AC+1，且∠ABC=60°．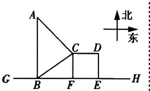
如图所示，GH是一条东西方向的公路，现准备在点B的正北方向的点A处建一仓库，设AB=y千米，并在公路旁边建造边长为x千米的正方形无顶中转站CDEF（其中边EF在公路GH上），现向公路和中转站分别修两条简易公路AB，AC，已知AB=AC+1，且∠ABC=60°．
km处，C村与B地相距4 km，且在B地的正东方向，已知公路PQ上任一点到B、C的距离之和都为8 km.现要在公路旁建造一个变电房M(变电房M可视为建在公路上)分别向A村、C村送电，但C村有一村办工厂，用电须用专用线路，不得与民用混线用电，因此向C村要架两条线路分别给村民和工厂送电，要使得所用电线最短，变电房M应建在A村的什么方位？并求出M到A村的距离.