Question

设为正整数，规定：，已知．

（1）解不等式：；

（2）设集合，对任意，证明：；

（3）求的值；

（4）若集合，证明：中至少包含有个元素．

Answer 1

解：（1）①当0≤≤1时，由≤得，≥．∴≤≤1．

            ②当1＜≤2时，因≤恒成立．∴1＜≤2．

            由①，②得，≤的解集为{|≤≤2}．

    （2）∵，，，

∴当时，；

  当时，；

  当时，．

即对任意，恒有．

（3），，

，

         ，

         一般地，（）．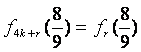

   （4）由（1）知，，∴．则．∴．

        由（2）知，对，或1，或2，恒有，∴．

则0，1，2．

        由（3）知，对，，， ，恒有，

∴，，，．

  综上所述，，0，1，2，，，，．∴中至少含有8个元素．