题目内容
设n为正整数,规定:fn(x)=
| ||
| n个f |
|
(1)解不等式:f(x)≤x;
(2)设集合A={0,1,2},对任意x∈A,证明:f3(x)=x;
(3)求f2008(
| 8 |
| 9 |
分析:(1)因为是分段函数,所以先根据定义域选择解析式来构造不等式,
当0≤x≤1时,由2(1-x)≤x求解;
当1<x≤2时,由x-1≤x求解,取后两个结果取并集.
(2)先求得f(0),f(1),f(2),
再分别求得f(f(0)),f(f(f(0)));f(f(1)),f(f(f(1)));
f(f(2)).再观察与自变量是否相等即可.
(3)看问题有2008重求值,一定用到周期性,所以先求出f1(
)=2(1-
)=
,f2(
)=f(f(
))=f(
)=
,f3(
)=f(f2(
))=f(
)=
-1=
,f4(
)=f(f3(
))=f(
)=2(1-
)=
,观察是以4为周期,有f4k+r(
)=fr(
)(k,r∈N)求解..
当0≤x≤1时,由2(1-x)≤x求解;
当1<x≤2时,由x-1≤x求解,取后两个结果取并集.
(2)先求得f(0),f(1),f(2),
再分别求得f(f(0)),f(f(f(0)));f(f(1)),f(f(f(1)));
f(f(2)).再观察与自变量是否相等即可.
(3)看问题有2008重求值,一定用到周期性,所以先求出f1(
| 8 |
| 9 |
| 8 |
| 9 |
| 2 |
| 9 |
| 8 |
| 9 |
| 8 |
| 9 |
| 2 |
| 9 |
| 14 |
| 9 |
| 8 |
| 9 |
| 8 |
| 9 |
| 14 |
| 9 |
| 14 |
| 9 |
| 5 |
| 9 |
| 8 |
| 9 |
| 8 |
| 9 |
| 5 |
| 9 |
| 5 |
| 9 |
| 8 |
| 9 |
| 8 |
| 9 |
| 8 |
| 9 |
解答:解:(1)①当0≤x≤1时,由2(1-x)≤x得,x≥
.
∴
≤x≤1.
②当1<x≤2时,因x-1≤x恒成立.
∴1<x≤2.
由①,②得,f(x)≤x的解集为{x|
≤x≤2}.
(2)∵f(0)=2,f(1)=0,f(2)=1,
∴当x=0时,f3(0)=f(f(f(0)))=f(-f(2))=f(1)=0;
当x=1时,f3(1)=f(f(f(1)))=f(f(0))=f(2)=1;
当x=2时,f3(2)=f(f(f(2)))=f(f(1))=f(0)=2.
即对任意x∈A,恒有f3(x)=x.
(3)f1(
)=2(1-
)=
,
f2(
)=f(f(
))=f(
)=
,
f3(
)=f(f2(
))=f(
)=
-1=
,
f4(
)=f(f3(
))=f(
)=2(1-
)=
,
一般地,f4k+r(
)=fr(
)(k,r∈N).
∴f2008(
)=f0(
)=
| 2 |
| 3 |
∴
| 2 |
| 3 |
②当1<x≤2时,因x-1≤x恒成立.
∴1<x≤2.
由①,②得,f(x)≤x的解集为{x|
| 2 |
| 3 |
(2)∵f(0)=2,f(1)=0,f(2)=1,
∴当x=0时,f3(0)=f(f(f(0)))=f(-f(2))=f(1)=0;
当x=1时,f3(1)=f(f(f(1)))=f(f(0))=f(2)=1;
当x=2时,f3(2)=f(f(f(2)))=f(f(1))=f(0)=2.
即对任意x∈A,恒有f3(x)=x.
(3)f1(
| 8 |
| 9 |
| 8 |
| 9 |
| 2 |
| 9 |
f2(
| 8 |
| 9 |
| 8 |
| 9 |
| 2 |
| 9 |
| 14 |
| 9 |
f3(
| 8 |
| 9 |
| 8 |
| 9 |
| 14 |
| 9 |
| 14 |
| 9 |
| 5 |
| 9 |
f4(
| 8 |
| 9 |
| 8 |
| 9 |
| 5 |
| 9 |
| 5 |
| 9 |
| 8 |
| 9 |
一般地,f4k+r(
| 8 |
| 9 |
| 8 |
| 9 |
∴f2008(
| 8 |
| 9 |
| 8 |
| 9 |
| 8 |
| 9 |
点评:本题主要考查求解分段函数构造的不等式,要注意分类讨论,还考查了分段函数多重求值,要注意从内到外,根据自变量取值选择好解析式.

练习册系列答案
相关题目
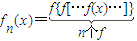 ,已知
,已知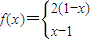
 .
.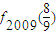 ;
;