题目内容
4．下列函数中，定义域为R的是（ ）| A． | y=$\sqrt{x}$ | B． | y=（x-1）0 | C． | y=x3+3 | D． | y=$\frac{1}{x}$ |
分析 分别求出选项中每个函数的定义域，即可得出正确的答案．
解答 解：对于A，y=$\sqrt{x}$的定义域是[0，+∞），∴不满足题意；
对于B，y=（x-1）0的定义域是（-∞，0）∪（0，+∞），∴不满足题意；
对于C，y=x3+3的定义域是（-∞，+∞），∴满足题意；
对于D，y=$\frac{1}{x}$的定义域是（-∞，0）∪（0，+∞），∴不满足题意．
故选：C．
点评 本题考查了根据函数的解析式求定义域的应用问题，是基础题目．
练习册系列答案
相关题目
18．若函数y=ax（a＞0且a≠1）在[0，1]上的最大值与最小值之和为3，则tan$\frac{a•180°}{6}$的值为（ ）
| A． | 0 | B． | $\frac{\sqrt{3}}{3}$ | C． | 1 | D． | $\sqrt{3}$ |
15．若logm7＜logn7＜0，那么m，n满足的条件是（ ）
| A． | 0＜n＜m＜1 | B． | n＞m＞1 | C． | m＞n＞1 | D． | 0＜m＜n＜1 |
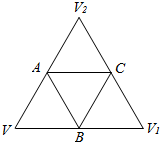某几何体的展开图如图所示（其中△VAB，△V1AC，△V2BC，△ABC都是边长为2的等边三角形）．将它沿AB、BC、AC折叠还原为原几何体，使得V、V1、V2重合于点V．