题目内容
等差数列{an}中,公差d不为0,且a1,a3,a9恰好是某等比数列的前三项.(1)求该等比数列的公比;
(2)这个等差数列中是否存在某一项恰好是这个等比数列的第四项,若存在,请求出是等差数列的第几项;若不存在,请说明理由.
【答案】分析:(1)由题意可得a32=a1•a9,从而建立关于公差d的方程,解方程可求d,进而求出等比数列的公比;
(2)确定数列的通项,即可求得结论.
解答:解:(1)∵等差数列{an}中,a1,a3,a9恰好是某等比数列的前三项
∴a32=a1•a9,
∴(a1+2d)2=a1•(a1+8d),∴d2=a1d,
∵d≠0,∴d,=a1,∴q=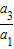 =3;
=3;
(2)由(1)知an=a1+(n-1)×a1=na1,
∵a1•33=27a1,
∴等差数列中第27项恰好是这个等比数列的第四项.
点评:本题考查了等差数列及等比数列的通项公式,考查学生的计算能力,属于基础题.
(2)确定数列的通项,即可求得结论.
解答:解:(1)∵等差数列{an}中,a1,a3,a9恰好是某等比数列的前三项
∴a32=a1•a9,
∴(a1+2d)2=a1•(a1+8d),∴d2=a1d,
∵d≠0,∴d,=a1,∴q=
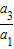 =3;
=3;(2)由(1)知an=a1+(n-1)×a1=na1,
∵a1•33=27a1,
∴等差数列中第27项恰好是这个等比数列的第四项.
点评:本题考查了等差数列及等比数列的通项公式,考查学生的计算能力,属于基础题.

练习册系列答案
相关题目