题目内容
已知集合A={x|2a＜x＜3-2a}，B={x|x＜5a+1}
（1）若A∪B=B，求a的取值范围；
（2）若A∩B=∅，求a的取值范围．
解：（1）因为集合A={x|2a＜x＜3-2a}，B={x|x＜5a+1}
A∪B=B，所以3-2a≤5a+1，解得a≥
，
所以a 的范围是[
）．
（2）因为A∩B=∅，所以2a≥5a+1，
解得a≤
，所以a的范围是（-
．
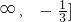分析：（1）利用A∪B=B，列出关系式，即可求出a的范围．
（2）通过A∩B=∅，列出a的关系式，然后求出a的范围．
点评：本题考查集合的基本运算，区间端点的比较，考查计算能力．
A∪B=B，所以3-2a≤5a+1，解得a≥
，所以a 的范围是[
）．（2）因为A∩B=∅，所以2a≥5a+1，
解得a≤
，所以a的范围是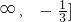（-．分析：（1）利用A∪B=B，列出关系式，即可求出a的范围．
（2）通过A∩B=∅，列出a的关系式，然后求出a的范围．
点评：本题考查集合的基本运算，区间端点的比较，考查计算能力．
练习册系列答案
智趣寒假作业云南科技出版社系列答案
相关题目