题目内容
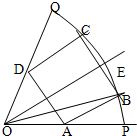 如图,已知OPQ是半径为1,圆心角为60°的扇形,∠POQ的平分线交弧PQ于点E,扇形POQ的内接矩形ABCD关于OE对称;设∠POB=α,矩形ABCD的面积为S.
如图,已知OPQ是半径为1,圆心角为60°的扇形,∠POQ的平分线交弧PQ于点E,扇形POQ的内接矩形ABCD关于OE对称;设∠POB=α,矩形ABCD的面积为S.(1)求S与α的函数关系f(α);
(2)求S=f(α)的最大值.
分析:(1)由题意可得△AOD为等边三角形,求得BC=2sin(
-α)=cosα-
sinα.再求得∠ABO=
-α,△OAB中,利用正弦定理求得AB=2sinα.
可得矩形ABCD的面积S=f(α)=AB•BC=2sinα(cosα-
sinα), (0<α<
).
(2)由(1)可得S=f(α)=2sin(2α+
)-
.再由 0<α<
,根据正弦函数的定义域和值域求得S=f(α)的最大值.
| π |
| 6 |
| 3 |
| π |
| 6 |
可得矩形ABCD的面积S=f(α)=AB•BC=2sinα(cosα-
| 3 |
| π |
| 6 |
(2)由(1)可得S=f(α)=2sin(2α+
| π |
| 3 |
| 3 |
| π |
| 6 |
解答:解:(1)由题意可得AB∥OE∥CD,∴∠POE=∠PAB=
,∴∠OAD=
=∠ADO,∠BOC=
-2α,△AOD为等边三角形.
故BC=2sin(
-α)=2(
cosα-
sinα)=cosα-
sinα.
再由∠ABO=π-∠AOB-∠OAD-∠BAD=π-α-
-
=
-α,△OAB中,利用正弦定理可得
=
,
即
=
,化简可得AB=2sinα.
故矩形ABCD的面积S=f(α)=AB•BC=2sinα(cosα-
sinα), (0<α<
).
(2)由(1)可得S=f(α)=2sinαcosα-2
sin2α=sin2α+
cos2α-
=2(
sin2α+
cos2α)-
=2sin(2α+
)-
.
再由 0<α<
可得
<2α+
<
,故当 2α+
=
,即当α=
时,S=f(α)取得最大值为2-
.
| π |
| 6 |
| π |
| 3 |
| π |
| 3 |
故BC=2sin(
| π |
| 6 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
再由∠ABO=π-∠AOB-∠OAD-∠BAD=π-α-
| π |
| 3 |
| π |
| 2 |
| π |
| 6 |
| AB |
| sin∠AOB |
| OB |
| sin∠OAB |
即
| AB |
| sinα |
| 1 | ||||
sin(
|
故矩形ABCD的面积S=f(α)=AB•BC=2sinα(cosα-
| 3 |
| π |
| 6 |
(2)由(1)可得S=f(α)=2sinαcosα-2
| 3 |
| 3 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
=2sin(2α+
| π |
| 3 |
| 3 |
再由 0<α<
| π |
| 6 |
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
| π |
| 3 |
| π |
| 2 |
| π |
| 12 |
| 3 |
点评:本题主要考查直角三角形中的边角关系、两角和差的三角公式、正弦函数的定义域和值域,正弦定理的应用,属于中档题.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
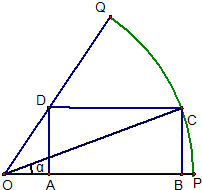 如图,已知OPQ是半径为1,圆心角为
如图,已知OPQ是半径为1,圆心角为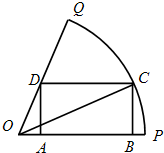 如图,已知OPQ是半径为为1,圆心角为
如图,已知OPQ是半径为为1,圆心角为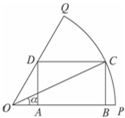 如图,已知OPQ是半径为1,圆心角为
如图,已知OPQ是半径为1,圆心角为 的扇形,C是扇形弧上的动点,ABCD是扇形的内接矩形.记∠COP=α,求当角α取何值时,矩形ABCD的面积最大?并求出这个最大面积.
的扇形,C是扇形弧上的动点,ABCD是扇形的内接矩形.记∠COP=α,求当角α取何值时,矩形ABCD的面积最大?并求出这个最大面积.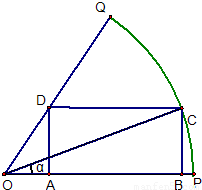 如图,已知OPQ是半径为1,圆心角为
如图,已知OPQ是半径为1,圆心角为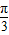 的扇形,C是扇形弧上的动点,ABCD是扇形的内接矩形.记∠COP=α,求当角α取何值时,矩形ABCD的面积最大?并求出这个最大面积.
的扇形,C是扇形弧上的动点,ABCD是扇形的内接矩形.记∠COP=α,求当角α取何值时,矩形ABCD的面积最大?并求出这个最大面积.