题目内容
11．已知函数f（x）=$\left\{\begin{array}{l}{\sqrt{2x-{x}^{2}，}}&{0≤x≤1}\\{-{x}^{2}，}&{-1≤x≤0}\end{array}\right.$，则函数f（x）图象与直线y=x围成的封闭图形的面积是$\frac{π}{4}+\frac{17}{24}$．分析 首先画出函数图象，找出函数f（x）的图象与直线y=x围成的封闭图形，利用定积分表示出其面积，然后计算即可．
解答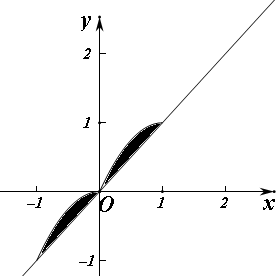 
解：由题意，函数f（x）的图象与直线y=x围成的封闭图形如图阴影部分，
曲线y=-x2与直线y=x的交点为（0，0），（-1，-1），
所以函数f（x）的图象与直线y=x围成的封闭图形的面积为S=$\frac{1}{4}$（π-$\frac{1}{2}×1×1$）+${∫}_{-1}^{0}（-{x}^{2}-x）dx$=$\frac{π}{4}$-$\frac{1}{8}$+（-$\frac{1}{3}{x}^{3}-\frac{1}{2}{x}^{2}）{|}_{-1}^{0}$${|}_{-1}^{0}$=$\frac{π}{4}+\frac{17}{24}$
故答案为：$\frac{π}{4}+\frac{17}{24}$．
点评 本题考查定积分知识的运用，关键是画出图形，利用定积分表示封闭图形的面积．
练习册系列答案
相关题目