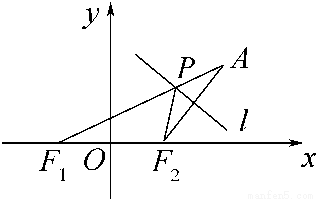
题目内容
已知点F
1（-1，0），F
2（1，0），动点P满足
|PF1|+|PF2|=2．
（1）求点P的轨迹C的方程；
（2）若直线l：y=kx+2与轨迹C交于A、B两点，且
•=0（其中O为坐标原点），求k的值．
分析：（1）由题意：|PF
1|+|PF
2|=2
＞|F
1F
2|，根据椭圆的定义即可求出点P的轨迹C的方程；
（2）将直线l方程与椭圆C联解消去y，得到关于x的一元二次方程，利用根与系数的关系结合数量积的坐标运算公式，建立关于k的方程，解之即可得到实数k的值．
解答：解：（1）∵点F
1（-1，0）、F
2（1，0），|PF
1|+|PF
2|=2
＞|F
1F
2|，
∴点P的轨迹C是以F
1、F
2为焦点且长轴2a=2
的椭圆，可得a=
，b=
=
因此，点P的轨迹C的方程为
+
=1．
（2）直线l：y=kx+2与
+
=1联列，消去y得：（3k
2+2）x
2+12kx+6=0，
设A（x
1，y
1），B（x
2，y
2），由根与系数关系可得
x
1+x
2=
，x
1x
2=
则y
1y
2=（kx
1+2）（kx
2+2）=k
2x
1x
2+2k（x
1+x
2）+4
=
-
+4=
∵
•=0，
∴x
1x
2+y
1y
2=0，即
+
=0，解之得k=±
点评：本题给出直线与椭圆相交于A、B两点，在A、B对原点的张角为90度时，求直线的斜率k之值．着重考查了平面向量数量积的运算、直线与圆锥曲线位置关系等知识，属于基础题．
练习册系列答案
相关题目
名校课堂系列答案
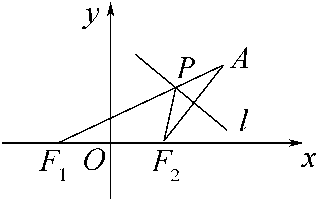已知点F1（-1，0），F2（1，0），动点A到点F1的距离是2
（2012•茂名一模）如图，设P是圆x2+y2=2上的动点，点D是P在x轴上的投影．M为线段PD上一点，且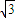
，线段AF2的中垂线l交AF1于点P．