题目内容
已知点F1(-1,0),F2(1,0),动点G满足|GF1|+|GF2|=2
.
(Ⅰ)求动点G的轨迹Ω的方程;
(Ⅱ)已知过点F2且与x轴不垂直的直线l交(Ⅰ)中的轨迹Ω于P、Q两点.在线段OF2上是否存在点M(m,0),使得以MP,MQ为邻边的平行四边形是菱形?若存在,求实数m的取值范围;若不存在,请说明理由.
| 2 |
(Ⅰ)求动点G的轨迹Ω的方程;
(Ⅱ)已知过点F2且与x轴不垂直的直线l交(Ⅰ)中的轨迹Ω于P、Q两点.在线段OF2上是否存在点M(m,0),使得以MP,MQ为邻边的平行四边形是菱形?若存在,求实数m的取值范围;若不存在,请说明理由.
分析:(Ⅰ)利用条件,根据椭圆的定义,可求动点G的轨迹Ω的方程;
(Ⅱ)设出直线l的方程与椭圆方程联立,根据MP,MQ为邻边的平行四边形是菱形,可得(
+
)⊥
,则有(
+
)•
=0,利用向量的数量积公式,结合韦达定理,即可求出实数m的取值范围.
(Ⅱ)设出直线l的方程与椭圆方程联立,根据MP,MQ为邻边的平行四边形是菱形,可得(
| MP |
| MQ |
| PQ |
| MP |
| MQ |
| PQ |
解答:解:(Ⅰ)由|GF1|+|GF2|=2
,且|F1F2|<2
知,动点G的轨迹是以F1(-1,0),F2(1,0)为焦点的椭圆,
设该椭圆的标准方程为
+
=1 (a>0, b>0),c=
,
由题知c=1,a=
,
则b2=a2-c2=2-1=1,
故动点G的轨迹Ω的方程是
+y2=1.(4分)
(Ⅱ)假设在线段OF2上存在M(m,0)(0<m<1),使得以MP、MQ为邻边的平行四边形是菱形.
直线l与x轴不垂直,设直线l的方程为y=k(x-1)(k≠0),
由
可得(1+2k2)x2-4k2x+2k2-2=0.
∴x1+x2=
,x1x2=
.(6分)
=(x1-m,y1),
=(x2-m,y2),
=(x2-x1,y2-y1),其中x2-x1≠0.
由于MP,MQ为邻边的平行四边形是菱形,
∴(
+
)⊥
,则有(
+
)•
=0,(8分)
从而(x2+x1-2m,y2+y1)•(x2-x1,y2-y1)=0,
∴(x2+x1-2m)(x2-x1)+(y2+y1)(y2-y1)=0,
又y=k(x-1),
则y2-y1=k(x2-x1),y2+y1=k(x2+x1-2),
故上式变形为(x2+x1-2m)+k2(x2+x1-2)=0,(10分)
将x1+x2=
代入上式,得(
-2m)+k2(
-2)=0,
即2k2-(2+4k2)m=0,
∴m=
(k≠0),可知0<m<
.
故实数m的取值范围是(0,
).(13分)
| 2 |
| 2 |
设该椭圆的标准方程为
| x2 |
| a2 |
| y2 |
| b2 |
| a2-b2 |
由题知c=1,a=
| 2 |
则b2=a2-c2=2-1=1,
故动点G的轨迹Ω的方程是
| x2 |
| 2 |
(Ⅱ)假设在线段OF2上存在M(m,0)(0<m<1),使得以MP、MQ为邻边的平行四边形是菱形.
直线l与x轴不垂直,设直线l的方程为y=k(x-1)(k≠0),
由
|
∴x1+x2=
| 4k2 |
| 1+2k2 |
| 2k2-2 |
| 1+2k2 |
| MP |
| MQ |
| PQ |
由于MP,MQ为邻边的平行四边形是菱形,
∴(
| MP |
| MQ |
| PQ |
| MP |
| MQ |
| PQ |
从而(x2+x1-2m,y2+y1)•(x2-x1,y2-y1)=0,
∴(x2+x1-2m)(x2-x1)+(y2+y1)(y2-y1)=0,
又y=k(x-1),
则y2-y1=k(x2-x1),y2+y1=k(x2+x1-2),
故上式变形为(x2+x1-2m)+k2(x2+x1-2)=0,(10分)
将x1+x2=
| 4k2 |
| 1+2k2 |
| 4k2 |
| 1+2k2 |
| 4k2 |
| 1+2k2 |
即2k2-(2+4k2)m=0,
∴m=
| k2 |
| 1+2k2 |
| 1 |
| 2 |
故实数m的取值范围是(0,
| 1 |
| 2 |
点评:本题考查轨迹方程,考查椭圆的定义,考查直线与椭圆的位置关系,考查向量知识的运用,考查学生分析转化问题的能力,属于中档题.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
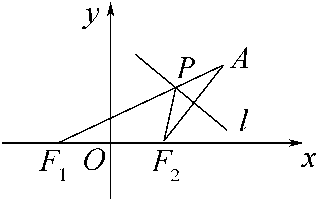 已知点F1(-1,0),F2(1,0),动点A到点F1的距离是2
已知点F1(-1,0),F2(1,0),动点A到点F1的距离是2 (2012•茂名一模)如图,设P是圆x2+y2=2上的动点,点D是P在x轴上的投影.M为线段PD上一点,且
(2012•茂名一模)如图,设P是圆x2+y2=2上的动点,点D是P在x轴上的投影.M为线段PD上一点,且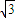 ,线段AF2的中垂线l交AF1于点P.
,线段AF2的中垂线l交AF1于点P.