题目内容
6.已知四棱锥P-ABCD的底面是菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD.(1)证明:平面PAC⊥平面PDB;
(2)求二面角P-AB-D的平面角的正切值.
分析 (1)由菱形性质得AC⊥BD,由线面垂直得AC⊥PD,由此能证明平面PAC⊥平面PDB.
(2)由已知得AD=AB=BD=PD,取AB中点E,连结DE,PE,∠PED是二面角P-AB-D的平面角,由此能求出P-AB-D的平面角的正切值.
解答 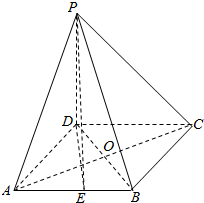 (1)证明:连结AC,BD,交于点O,
(1)证明:连结AC,BD,交于点O,
∵四棱锥P-ABCD的底面是菱形,∴AC⊥BD,
∵PD⊥平面ABCD,∴AC⊥PD,
∵PD∩BD=D,∴AC⊥平面PDB,
∵AC?平面PAC,∴平面PAC⊥平面PDB.
(2)解:∵四棱锥P-ABCD的底面是菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD,
∴AD=AB=BD=PD,
设AB=2,取AB中点E,连结DE,PE,
则DE⊥AB,PE⊥AB,
∴∠PED是二面角P-AB-D的平面角,
∵PD=AB=2,DE=$\sqrt{A{D}^{2}-A{E}^{2}}$=$\sqrt{4-1}=\sqrt{3}$,
∴tan∠PED=$\frac{PD}{DE}$=$\frac{2}{\sqrt{3}}$=$\frac{2\sqrt{3}}{3}$,
∴P-AB-D的平面角的正切值为$\frac{2\sqrt{3}}{3}$.
点评 本小题主要考查面面垂直的证明,考查二面角的正切值的法,考查空间中的线面关系,四棱锥的有关概念及勾股定理等基础知识,考查空间想象能力和推理能力.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
16.函数f(x)=log${\;}_{\frac{1}{4}}$(x2-9)的单调增区间是( )
| A. | (0,+∞) | B. | (-∞,0) | C. | (3,+∞) | D. | (-∞,-3) |
11.已知等比数列{an}的公比为q,Sn是{an}的前n项和,且满足:an+1=a1Sn+1(n∈N*),则下列结论正确的是( )
| A. | a1=2 | B. | a12<2015 | C. | q=2 | D. | S10>2015 |
18.已知四棱锥P-ABCD的底面ABCD是矩形,PA⊥底面ABCD,点E、F是棱PC、PD的中点,则:①AB⊥PD;②平面PBC与平面ABCD垂直;③△PCD的面积大于△PAB的面积;④直线AE与直线BF是异面直线.其中正确结论的序号是( )
| A. | ①② | B. | ①④ | C. | ②④ | D. | ①③ |
15.已知一个四面体其中五条棱的长分别为1,1,1,1,$\sqrt{2}$,则此四面体体积的最大值是( )
| A. | $\frac{{\sqrt{3}}}{12}$ | B. | $\frac{{\sqrt{2}}}{12}$ | C. | $\frac{{\sqrt{2}}}{4}$ | D. | $\frac{{\sqrt{3}}}{3}$ |