题目内容
11.已知等比数列{an}的公比为q,Sn是{an}的前n项和,且满足:an+1=a1Sn+1(n∈N*),则下列结论正确的是( )| A. | a1=2 | B. | a12<2015 | C. | q=2 | D. | S10>2015 |
分析 由已知条件推导出等比数列{an}的首项为1,公比为2,由此能求出结果.
解答 解:∵等比数列{an}的公比为q,Sn是{an}的前n项和,且满足:an+1=a1Sn+1(n∈N*),
∴a2=${{a}_{1}}^{2}+1$,${a}_{3}={a}_{1}({a}_{1}+{{a}_{1}}^{2}+1)+1={{a}_{1}}^{3}+{{a}_{1}}^{2}$+a1+1,
∴(${{a}_{1}}^{2}+1$)2=a1(${{a}_{1}}^{3}+{{a}_{1}}^{2}+{a}_{1}+1$),
解得a1=1,故A错误;
当a1=1时,a2=a1•a1+1=1+1=2,
q=$\frac{{a}_{2}}{{a}_{1}}=2$,故C正确;
${a}_{12}=1×{2}^{11}$=2048>2015,故B错误;
${S}_{10}=\frac{1-{2}^{10}}{1-2}$=1023<2015,故D错误.
故选:C.
点评 本题考查命题真假的判断,是基础题,解题时要认真审题,注意等比数列的性质的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.使|x-4|+|x-3|<a有实数解a的取值范围是( )
| A. | a>7 | B. | 1<a<7 | C. | a>1 | D. | a<7 |
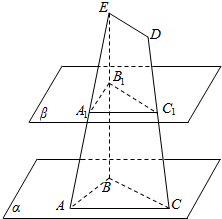 平面α内有△ABC,AB=5,BC=8,AC=7,梯形BCDE的底DE=2,过EB的中点B1的平面β∥α,若β分别交EA、DC于A1、C1,求△A1B1C1的面积.
平面α内有△ABC,AB=5,BC=8,AC=7,梯形BCDE的底DE=2,过EB的中点B1的平面β∥α,若β分别交EA、DC于A1、C1,求△A1B1C1的面积.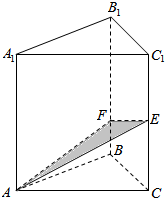 在直三棱柱ABC-A1B1C1中,底面三角形ABC为等腰直角三角形,且∠ABC=90°,E为C1C的中点,点F是BB1上是BF=$\frac{1}{4}$BB1,AC=AA1=2a,求平面EFA与面ABC所成角的大小.
在直三棱柱ABC-A1B1C1中,底面三角形ABC为等腰直角三角形,且∠ABC=90°,E为C1C的中点,点F是BB1上是BF=$\frac{1}{4}$BB1,AC=AA1=2a,求平面EFA与面ABC所成角的大小.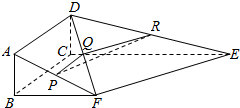 如图,四边形ABCD是矩形,四边形BCEF是直角梯形,平面ABCD⊥平面BCEF,∠FBC是直角,AB=1,BC=BF=2,CE=4,P、Q、R分别是AF、DF、DE的中点.
如图,四边形ABCD是矩形,四边形BCEF是直角梯形,平面ABCD⊥平面BCEF,∠FBC是直角,AB=1,BC=BF=2,CE=4,P、Q、R分别是AF、DF、DE的中点.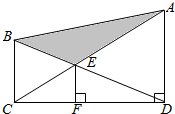 如图,直角梯形上、下底的和是14厘米,阴影部分面积是12平方厘米,EF是3厘米,求梯形面积.
如图,直角梯形上、下底的和是14厘米,阴影部分面积是12平方厘米,EF是3厘米,求梯形面积.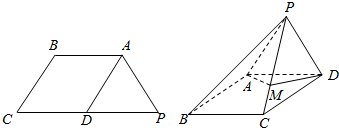 已知梯形ABCP,如图(1)所示,D是CP边的中点,AB∥PC,且2AB=PC,△APD为等边三角形,现将平面APD沿AD翻折,使平面APD⊥平面ABCD,得到如图(2)所示的四棱锥P-ABCD,点M在棱PC上,且PM=$\sqrt{3}$MC.
已知梯形ABCP,如图(1)所示,D是CP边的中点,AB∥PC,且2AB=PC,△APD为等边三角形,现将平面APD沿AD翻折,使平面APD⊥平面ABCD,得到如图(2)所示的四棱锥P-ABCD,点M在棱PC上,且PM=$\sqrt{3}$MC.