题目内容
【题目】数列{an}中, ![]() . (Ⅰ)求a1 , a2 , a3 , a4;
. (Ⅰ)求a1 , a2 , a3 , a4;
(Ⅱ)猜想an的表达式,并用数学归纳法加以证明.
【答案】解:(Ⅰ)∵ ![]() ,∴
,∴ ![]() ,即a1=1, ∵
,即a1=1, ∵ ![]() ,即a1+a2=4﹣a2﹣1,∴a2=1,
,即a1+a2=4﹣a2﹣1,∴a2=1,
∵ ![]() ,即a1+a2+a3=4﹣a3﹣
,即a1+a2+a3=4﹣a3﹣ ![]() ,∴a3=
,∴a3= ![]() ,
,
∵ ![]() ,即a1+a2+a3+a4=4﹣a4﹣
,即a1+a2+a3+a4=4﹣a4﹣ ![]() ,∴a3=
,∴a3= ![]() ,
,
(Ⅱ)猜想 ![]()
证明如下:①当n=1时,a1=1,此时结论成立;
②假设当n=k(k∈N*)结论成立,即 ![]() ,
,
那么当n=k+1时,有 ![]()
∵ ![]()
∴ ![]() ,
,
这就是说n=k+1时结论也成立.
根据①和②,可知对任何n∈N*时 ![]() .
.
【解析】(1)由 ![]() .我们依次将n=1,2,3,4…代入,可以求出a1 , a2 , a3 , a4;(2)观察(1)的结论,我们可以推断出an的表达式,然后由数学归纳法的步骤,我们先判断n=1时是否成立,然后假设当n=k时,公式成立,只要能证明出当n=k+1时,公式成立即可得到公式对所有的正整数n都成立.
.我们依次将n=1,2,3,4…代入,可以求出a1 , a2 , a3 , a4;(2)观察(1)的结论,我们可以推断出an的表达式,然后由数学归纳法的步骤,我们先判断n=1时是否成立,然后假设当n=k时,公式成立,只要能证明出当n=k+1时,公式成立即可得到公式对所有的正整数n都成立.
【考点精析】解答此题的关键在于理解数列的前n项和的相关知识,掌握数列{an}的前n项和sn与通项an的关系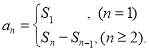 ,以及对数学归纳法的定义的理解,了解数学归纳法是证明关于正整数n的命题的一种方法.
,以及对数学归纳法的定义的理解,了解数学归纳法是证明关于正整数n的命题的一种方法.

练习册系列答案
相关题目
【题目】某省数学学业水平考试成绩分为A、B、C、D四个等级,在学业水平成绩公布后,从该省某地区考生中随机抽取60名考生,统计他们的数学成绩,部分数据如下:
等级 | A | B | C | D |
频数 | 24 | 12 | ||
频率 | 0.1 |
(1)补充完成上述表格中的数据;
(2)现按上述四个等级,用分层抽样的方法从这60名考生中抽取10名,在这10名考生中,从成绩A等和B等的所有考生中随机抽取2名,求至少有一名成绩为A等的概率.