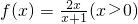题目内容
已知x>1,求证:x>ln(1+x).
证明:设f(x)=x-ln(1+x),
∵f′(x)=1-![]() =
=![]() ,x>1,
,x>1,
∴f′(x)>0.∴f(x)在(1,+∞)上是增函数.
又f(1)=1-ln2>1-lne=0,即f(1)>0,
∴f(x)>0,即x>ln(1+x)(x>1).
点评:(1)构造函数,借助导数确定单调性,这种证明不等式的方法经常使用,它是作差法的一个延伸.
(2)f(1)≥0是判断大小的重要依据,它的证明是本题的一个难点.

练习册系列答案
相关题目