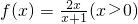题目内容
已知x＞1，求证：x＞1n（1+x）．
令函数f（x）=x-ln（1+x），（ x＞1），则f′（x）=1-
=
＞0，
故函数f（x）在（1，+∞）上是增函数．
再由f（1）=1-ln2＞0，可得f（x）＞0，故有x＞1n（1+x）．
| 1 |
| 1+x |
| x |
| 1+x |
故函数f（x）在（1，+∞）上是增函数．
再由f（1）=1-ln2＞0，可得f（x）＞0，故有x＞1n（1+x）．
练习册系列答案
阅读快车系列答案
相关题目
