题目内容
二次函数f(x)=ax2+bx+1(a>0),设f(x)=x的两个实根为x1,x2.
(1)如果b=2且|x2-x1|=2,求a的值;
(2)如果x1<2<x2<4,设函数f(x)的对称轴为x=x0,求证:x0>-1.
解析 (1)当b=2时,f(x)=ax2+2x+1(a>0).
方程f(x)=x为ax2+x+1=0.
|x2-x1|=2⇒(x2-x1)2=4⇒(x1+x2)2-4x1x2=4.
由韦达定理,可知
x1+x2=-![]() ,x1x2=
,x1x2=![]() .
.
代入上式,可得4a2+4a-1=0.
解得a=![]() ,a=
,a=![]() (舍去).
(舍去).
(2)证明:∵ax2+(b-1)x+1=0(a>0)的两根满足x1<2<x2<4,
设g(x)=ax2+(b-1)x+1,
∴![]() 即
即![]() ⇒
⇒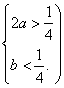
∴2a-b>0.
又∵函数f(x)的对称轴为x=x0,
∴x0=-![]() >-1.
>-1.

练习册系列答案
相关题目
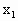 )(x-
)(x- )(a<0)的最大值是________.
)(a<0)的最大值是________.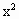 +bx(a,b是常数且a≠0)满足条件:f(2)=0且方程f(x)=x有等根.(1)求f(x)的解析式;(2)问是否存在实数m,n(m<n),使f(x)的定义域和值域分别为[m,n]和[2m,2n],如存在,求出m,n的值;如不存在,说明理由.
+bx(a,b是常数且a≠0)满足条件:f(2)=0且方程f(x)=x有等根.(1)求f(x)的解析式;(2)问是否存在实数m,n(m<n),使f(x)的定义域和值域分别为[m,n]和[2m,2n],如存在,求出m,n的值;如不存在,说明理由. +bx+c
+bx+c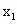 、
、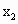 ∈R.且
∈R.且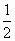 [f(
[f(