题目内容
(12分)如图,在正方体![]() 中,
中,![]() 为
为![]() 中点,
中点,![]() ∩
∩![]() 于
于![]() 。
。
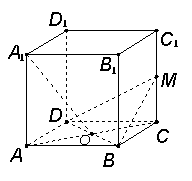 求证:
求证:![]() ⊥平面
⊥平面![]() 。
。
(12分)证明:连结A1B,A1D,在正方形中,A1B=A1D,O是BD中点,
∴A1O⊥BD;连结OM,A1M,A1C1, K^S*5U.
设AB=a,则AA1=a,MC=![]() a=MC1,OA=OC=
a=MC1,OA=OC=![]() a,AC=
a,AC=![]() a,
a,
∴A1O2=A1A2+AO2=a2+![]() a2=
a2=![]() a2,OM2=OC2+MC2=
a2,OM2=OC2+MC2=![]() a2,A1M2=A1C12+MC12=2a2+
a2,A1M2=A1C12+MC12=2a2+![]() a2=
a2=![]() a2,
a2,
∴A1M2=A1O2+OM2,∴A1O⊥OM,∴AO1⊥平面MBD。

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 中,
中, 为对角线
为对角线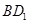 的三等分点,
的三等分点,
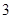 个 B.
个 B. 个
个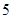 个 D.
个 D. 个
个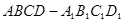 中,
中,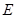 为
为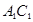 的中点,则异面直线
的中点,则异面直线 与
与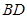 所成的角为( )
所成的角为( )
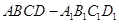 中,
中, 为底面
为底面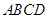 的中心,
的中心, 是
是 的中点,设
的中点,设 是
是 上的中点,求证:(1)
上的中点,求证:(1) ;
; ∥平面
∥平面 .
.
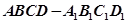 中,
中,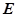 为棱
为棱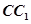 的中点,
的中点,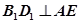 ;
;  的正切值.
的正切值.