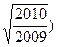题目内容
选修4—1：几何证明选讲
如图，已知四边形ABCD内接于⊙O，EF//CD，FG切⊙O于点G.
求证EF=FG.
如图，已知四边形ABCD内接于⊙O，EF//CD，FG切⊙O于点G.
求证EF=FG.
证明：因为FG切⊙O于点G，所以FG2＝FB·FA． ……………………………2分
因为EF∥CD，所以∠BEF=∠ECD．
又A、B、C、D四点共圆，所以∠ECD=∠EAF，所以∠BEF=∠EAF．………5分
又∠EFA=∠BFE，所以△EFA∽△BFE． ………………………………7分
所以＝，即EF2＝FB·FA．
所以FG2= EF2，即EF=FG.．…………………………………………………………10分
因为EF∥CD，所以∠BEF=∠ECD．
又A、B、C、D四点共圆，所以∠ECD=∠EAF，所以∠BEF=∠EAF．………5分
又∠EFA=∠BFE，所以△EFA∽△BFE． ………………………………7分
所以＝，即EF2＝FB·FA．
所以FG2= EF2，即EF=FG.．…………………………………………………………10分
略
练习册系列答案
宝贝计划期末冲刺夺100分系列答案
能考试全能100分系列答案
相关题目
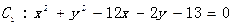和圆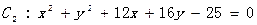
的公共弦为直径的圆的方程。
都经过A、B两点，AC是⊙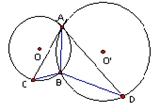
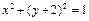
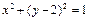
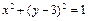
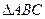内接于圆O，点D在OC的延长线上，AD是圆O的切线，若
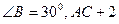，则OD的长为 。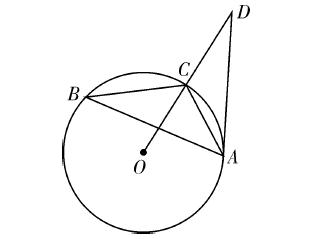
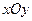=60o,平面上任意一点P的斜坐标是这样定义的：若
（
，
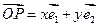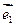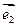分别是与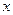
，
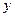轴同方向的单位向量），则P点的斜坐标为（
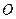为圆心，2为半径的圆的方程为（ ）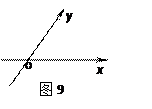
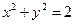
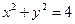
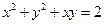
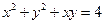
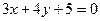相切的圆的标准方程是 
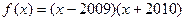的图像与
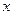轴、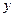
轴有三个不同的交点，有一个圆恰好经过这三个点，则此圆与坐标轴的另一个交点是 （ ）
