题目内容
(本题满分16分)本题共有2个小题,第1小题满分8分,第2小题满分8分.
已知双曲线![]() 设过点
设过点![]() 的直线l的方向向量
的直线l的方向向量![]()
(1) 当直线l与双曲线C的一条渐近线m平行时,求直线l的方程及l与m的距离;
(2) 证明:当![]() >
>![]() 时,在双曲线C的右支上不存在点Q,使之到直线l的距离为
时,在双曲线C的右支上不存在点Q,使之到直线l的距离为![]() .
.
(1)双曲线C的渐近线![]() ,即
,即![]() …… 2分
…… 2分
![]() 直线
直线![]() 的方程
的方程![]() …… 6分
…… 6分
![]() 直线
直线![]() 与m的距离
与m的距离![]() …… 8分
…… 8分
(2)![]() 设过原点且平行于
设过原点且平行于![]() 的直线
的直线![]()
则直线![]() 与
与![]() 的距离
的距离![]()
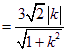 ,
,
当![]() 时,
时,![]() . …… 12分
. …… 12分
又双曲线C的渐近线为![]() ,
,
![]() 双曲线C的右支在直线
双曲线C的右支在直线![]() 的右下方,
的右下方,
![]() 双曲线C的右支上的任意点到直线
双曲线C的右支上的任意点到直线![]() 的距离大于
的距离大于![]() .
.
故在双曲线C的右支上不存在点Q![]() 到到直线
到到直线![]() 的距离为
的距离为![]() …… 16分
…… 16分
![]() 假设双曲线C右支上存在点Q
假设双曲线C右支上存在点Q![]() 到到直线
到到直线![]() 的距离为
的距离为![]() ,
,
|
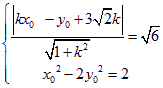 , (1)
, (1) 由(1)得![]() , …… 11分
, …… 11分
设![]()
当![]() 时,
时,![]() :
:
![]() …… 13分
…… 13分
将![]() 代入(2)得
代入(2)得![]() ,
,
![]()
![]() ,
,![]()
![]()
![]()
故在双曲线C的右支上不存在点Q![]() 到到直线
到到直线![]() 的距离为
的距离为![]() …… 16分
…… 16分
解析:
⑴中知道双曲线的方程可以求出渐近线方程,因为直线l和渐近线平行,所以可以确定l的方程,直线l与m方程确定,可以利用两条平行线间的距离公式求出距离.⑵是一个存在性问题,可以寻找参考对象,也可用反证法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 为偶函数, 且
为偶函数, 且
 的值;
的值; 为三角形
为三角形 的一个内角,求满足
的一个内角,求满足 的
的 为偶函数, 且
为偶函数, 且
 的值;
的值; 为三角形
为三角形 的一个内角,求满足
的一个内角,求满足 的
的