题目内容
给出下列命题:
①若“p∧q”与“p∨q”都是假命题,则“?p∧?q”是真命题;
②x2≠y2?x≠y或x≠-y;
③命题“a、b都不是偶数,则a+b不是偶数”的逆否命题是“若a+b是偶数,则a、b都是偶数”;
④若关于x的实数不等式ax2+bx+c≤0的解集是R,则必有a<0且△≤0.
其中正确的是
①若“p∧q”与“p∨q”都是假命题,则“?p∧?q”是真命题;
②x2≠y2?x≠y或x≠-y;
③命题“a、b都不是偶数,则a+b不是偶数”的逆否命题是“若a+b是偶数,则a、b都是偶数”;
④若关于x的实数不等式ax2+bx+c≤0的解集是R,则必有a<0且△≤0.
其中正确的是
①
①
(写出序号)分析:根据复合命题真假判断的真值表,可以判断出①的真假;根据实数的性质写出x2≠y2的等价命题,可以判断出②的真假;根据偶数和奇数的性质,可以判断命题③的真假;根据函数恒成立问题及二次函数的图象和性质,可以判断命题④的真假,进而得到答案.
解答:解:若“p∧q”与“p∨q”都是假命题,则命题p,q均为假命题,则命题?p,?q均为真命题,则“?p∧?q”是真命题,故①正确;
x2≠y2?x≠y且x≠-y,故②错误;
命题“a、b都不是偶数,则a+b不是偶数”的逆否命题是“若a+b是偶数,则a、b中存在偶数“,故③错误;
若关于x的实数不等式ax2+bx+c≤0的解集是R,则必有a=b=0,c≤0或a<0且△≤0,故④错误;
故答案为:①
x2≠y2?x≠y且x≠-y,故②错误;
命题“a、b都不是偶数,则a+b不是偶数”的逆否命题是“若a+b是偶数,则a、b中存在偶数“,故③错误;
若关于x的实数不等式ax2+bx+c≤0的解集是R,则必有a=b=0,c≤0或a<0且△≤0,故④错误;
故答案为:①
点评:本题考查的知识点是命题的真假判断与应用,其中判断出每个命题的真假是解答本题的关键,其中④中易忽略a=b=0,c≤0的情况,而误判为正确.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
 、
、 ,两个不同平面
,两个不同平面 、
、 ,给出下列命题:
,给出下列命题:
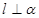 ,则
,则 则
则 在平面
在平面 。
。 ,对任意
,对任意 ,运算“
,运算“ ”具有如下性质:
”具有如下性质: ; (2)
; (2) ; (3)
; (3) .
. :
: ,则
,则 ;
; ,且
,且 ,则a = 0;
,则a = 0; ,且
,且 ,
, ,则a = c.
,则a = c. 和
和 为不重合的两个平面,给出下列命题:1若
为不重合的两个平面,给出下列命题:1若 与
与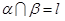 ,若
,若 ;4直线
;4直线 的充要条件是
的充要条件是 、
、 ,且m⊥
,且m⊥ ,
,