题目内容
已知两条不同直线 、
、 ,两个不同平面
,两个不同平面 、
、 ,给出下列命题:
,给出下列命题:
(1)若

 ,
,

 且
且 ∥
∥ ,则
,则 ∥
∥ ;(2)若
;(2)若

 ,
,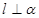 ,则
,则 ⊥
⊥ ;
;
(3)若 ∥
∥ ,则
,则 平行于
平行于 内的所有直线;(4)若
内的所有直线;(4)若 则
则 ⊥
⊥ ;
;
(5)若 在平面
在平面 内的射影互相垂直,则
内的射影互相垂直,则 。
。
其中正确命题的序号是 (把你认为正确命题的序号都填上).
【答案】
(2)(4)
【解析】
试题分析:因为(1)若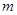
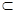
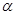 ,
,
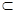
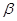 且
且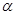 ∥
∥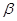 ,则
,则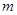 ∥
∥ ;根据面面平行的性质定理可知,也可能平行也可能异面直,不成立。
;根据面面平行的性质定理可知,也可能平行也可能异面直,不成立。
(2)若
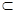
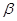 ,
, ,则
,则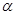 ⊥
⊥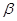 ;利用面面垂直的判定定理可知成立。
;利用面面垂直的判定定理可知成立。
(3)若 ∥
∥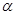 ,则
,则 平行于
平行于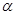 内的所有直线;一条直线平行于平面,可能与平面内的直线的关于平行,也可能异面,不成立。
内的所有直线;一条直线平行于平面,可能与平面内的直线的关于平行,也可能异面,不成立。
(4)若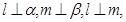 则
则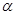 ⊥
⊥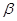 ;由面面垂直的判定定理可知,成立。
;由面面垂直的判定定理可知,成立。
(5)若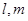 在平面
在平面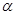 内的射影互相垂直,则
内的射影互相垂直,则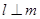 。可能是斜交,故不成立。
。可能是斜交,故不成立。
故填写(2)(4)
考点:本题主要是考查空间中点线面的位置关系的判定和运用。
点评:解决该试题的关键是这种题目只要举出不正确选项中的反例就可以确定结论,注意题目中包含的线和面比较多,用实物演示可以更加形象.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目