题目内容
若函数 (a为常数)在定义域上是增函数,则实数a的取值范围是 .
(a为常数)在定义域上是增函数,则实数a的取值范围是 .
【答案】分析:确定函数的定义域,求导函数令其大于等于0,再分离参数,利用基本不等式,即可求实数a的取值范围.
解答:解:函数的定义域为(0,+∞),求导数可得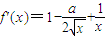
∵函数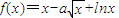 (a为常数)在定义域上是增函数,
(a为常数)在定义域上是增函数,
∴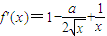 ≥0在(0,+∞)上恒成立
≥0在(0,+∞)上恒成立
∴
∵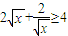
∴a≤4
∴实数a的取值范围是(-∞,4]
故答案为(-∞,4].
点评:本题考查导数知识的运用,考查函数的单调性,考查分离参数,利用基本不等式求最值.
解答:解:函数的定义域为(0,+∞),求导数可得
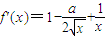
∵函数
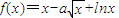 (a为常数)在定义域上是增函数,
(a为常数)在定义域上是增函数,∴
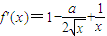 ≥0在(0,+∞)上恒成立
≥0在(0,+∞)上恒成立∴

∵
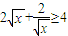
∴a≤4
∴实数a的取值范围是(-∞,4]
故答案为(-∞,4].
点评:本题考查导数知识的运用,考查函数的单调性,考查分离参数,利用基本不等式求最值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
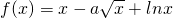 (a为常数)在定义域上是增函数,则实数a的取值范围是________.
(a为常数)在定义域上是增函数,则实数a的取值范围是________.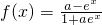 (a为常数)在定义上为奇函数,则实数a等于________.
(a为常数)在定义上为奇函数,则实数a等于________.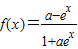 (a为常数)在定义上为奇函数,则实数a等于 .
(a为常数)在定义上为奇函数,则实数a等于 .