题目内容
在一场娱乐晚会上, 有5位民间歌手(1至5号)登台演唱, 由现场数百名观众投票选出最受欢迎歌手.各位观众须彼此独立地在选票上选3名选手, 其中观众甲是1号歌手的歌迷, 他必选1号, 不选2号, 另在3至5号中随机选2名.观众乙和丙对5位歌手的演唱没有偏爱, 因此在1至5号中随机选3名歌手.
(1)求观众甲选中3号歌手且观众乙未选中3号歌手的概率;
(2)X表示3号歌手得到观众甲、乙、丙的票数之和, 求X的分布列和数学期望.
(1)求观众甲选中3号歌手且观众乙未选中3号歌手的概率;
(2)X表示3号歌手得到观众甲、乙、丙的票数之和, 求X的分布列和数学期望.
(1)
(2)


(2)
| X | 0 | 1 | 2 | 3 |
| P | 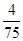 |  | 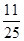 | 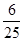 |

本题考查涉及排列组合、概率、随机变量分布列和期望问题,(1)问中考查了“观众甲选中3号歌手且观众乙未选中3号歌手”互斥事件同时发生的概率,也可以利用树形图解决。(2)问中要注意分布列性质运用,验证概率总合是否为1。此类问题在高考中属于常考重点题型,必须熟练掌握。
(1)由于观众甲必选1,不选2,则观众甲选中3号歌手的概率为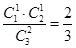 ,观众乙未选中3号歌手的概率为
,观众乙未选中3号歌手的概率为 ,甲乙选票彼此独立,故观众甲选中3号歌手且观众乙未选中3号歌手的概率为
,甲乙选票彼此独立,故观众甲选中3号歌手且观众乙未选中3号歌手的概率为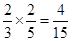 .
.
(2)X的所有可能取值为0,1,2,3.由(1)知,观众甲选中3号歌手的概率为 ,观众乙选中3号歌手的概率为
,观众乙选中3号歌手的概率为 ,则观众丙选中3号歌手的概率也为
,则观众丙选中3号歌手的概率也为 ,则
,则
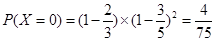 ,
, ,
,
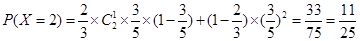 ,
, .
.
则X的分布列如下:
 。
。
点评:本题考查排列组合、概率、随机变量分布列和期望问题。属于中档题。
(1)由于观众甲必选1,不选2,则观众甲选中3号歌手的概率为
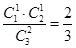 ,观众乙未选中3号歌手的概率为
,观众乙未选中3号歌手的概率为 ,甲乙选票彼此独立,故观众甲选中3号歌手且观众乙未选中3号歌手的概率为
,甲乙选票彼此独立,故观众甲选中3号歌手且观众乙未选中3号歌手的概率为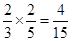 .
.(2)X的所有可能取值为0,1,2,3.由(1)知,观众甲选中3号歌手的概率为
 ,观众乙选中3号歌手的概率为
,观众乙选中3号歌手的概率为 ,则观众丙选中3号歌手的概率也为
,则观众丙选中3号歌手的概率也为 ,则
,则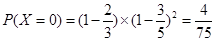 ,
, ,
,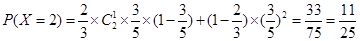 ,
, .
.则X的分布列如下:
| X | 0 | 1 | 2 | 3 |
| P | 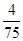 |  | 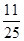 | 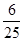 |
 。
。点评:本题考查排列组合、概率、随机变量分布列和期望问题。属于中档题。

练习册系列答案
相关题目
 的有8人.
的有8人.
 的值及甲班学生每天平均学习时间在区间
的值及甲班学生每天平均学习时间在区间 的人数;
的人数; ,求
,求



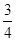
 ,求n的最大值;
,求n的最大值;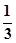 ,用
,用 表示小李射击
表示小李射击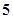 次击中目标的次数,则
次击中目标的次数,则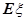 与方差
与方差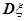 的值分别是______________________.
的值分别是______________________.