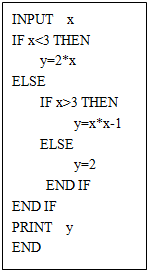若函数f(x)=-$\frac{1}{3}$x3+$\frac{1}{2}$x2+2ax在[$\frac{2}{3}$.+∞)上存在单调递增区间.则a的取值范围是$$．题目和参考答案——青夏教育精英家教网——

题目内容

11．若函数f（x）=-$\frac{1}{3}$x³+$\frac{1}{2}$x²+2ax在[$\frac{2}{3}$，+∞）上存在单调递增区间，则a的取值范围是$（-\frac{1}{9}，+∞）$．

分析求出函数的导数，利用导函数值大于0，转化为a的表达式，求出最值即可得到a的范围．

解答解：函数f（x）=-$\frac{1}{3}$x³+$\frac{1}{2}$x²+2ax，
f′（x）=-x²+x+2a=-（x-$\frac{1}{2}$）²+$\frac{1}{4}$+2a．
当x∈[$\frac{2}{3}$，+∞）时，f′（x）的最大值为f′（$\frac{2}{3}$）=2a+$\frac{2}{9}$，令2a+$\frac{2}{9}$＞0，解得a$＞-\frac{1}{9}$，
所以a的取值范围是$（-\frac{1}{9}，+∞）$．
故答案为：$（-\frac{1}{9}，+∞）$．

点评本题考查函数的导数的应用，考查计算能力．

练习册系列答案

优加学习方案系列答案

52045模块式全能训练系列答案

钟书金牌新教材全练系列答案

4560课时双测系列答案

百所名校精点试题系列答案

互动课堂系列答案

完美课堂系列答案

激活思维智能训练课时导学练系列答案

练出好成绩系列答案

全效学习课时提优系列答案

相关题目

1．已知A，B，C，D，E是球面上的五个点，其中A，B，C，D在同一圆周上，若E不在A，B，C，D所在的圆周上，则从这五个点的任意两点的连线中取出2条，这两条直线是异面直线的概率是（　　）

2．已知4x²-ax+1可变成（2x-b）²的形式，则ab=4．

19．如图是一段程序它的功能是求函数y=$\left\{\begin{array}{l}{2x}&{x＜3}\\{\stackrel{2}{{x}^{2}-1}}&{\stackrel{x=3}{x＞3}}\end{array}\right.$的函数值．

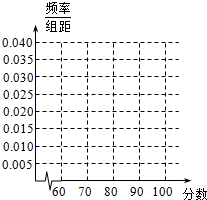为纪念中国抗日战争胜利70周年，某中学高三年级举办了“铭记历史，开创未来”的抗战历史知识竞赛活动，共有1000名学生参加了这次竞赛．为了解本次竞赛的成绩情况，从中抽取了部分学生的成绩（得分均为整数，满分为100分）进行统计，请你根据频率分布表，解答下列问题：

序号	分组	频数	频率
1	[60，70）	①	0.15
2	[70，80）	20	0.2
3	[80，90）	35	0.35
4	[90，100）	30	②
合计		100	1

（1）写出频率分布表中①、②所代表的数据；
（2）在所给坐标系中画出样本的频率分布直方图；
（3）为鼓励更多的学生了解“抗战历史”知识，对成绩不低于90分的学生给予奖励，请估计在参加竞赛的1000名学生中大概有多少名学生获奖．

16．已知函数f（x）=x（e^x+2x-1）+$\frac{1}{2}$．
（1）求证：函数F（x）=f（x）-x³-$\frac{1}{2}$仅有一个零点；
（2）记max{a，b}表示a，b中更大的数，比如max{3，-1}=3，max{$\sqrt{2}$，$\sqrt{2}$}=$\sqrt{2}$．设g（x）=ln|x|-|x|+1，h（x）=max{f（x），g（x）}（x≠0），求证：h（x）＞$\frac{3e-8}{8e}$．

3．关于下列说法
①描述算法可以有不同的方式；
②方差和标准差具有相同的单位；
③根据样本估计总体，其误差与所选择的样本容量无关；
④从总体中可以抽取不同的几个样本；
⑤如果容量相同的两个样本的方差满足$S_1^2＜S_2^2$，那么推得总体也满足$S_1^2＜S_2^2$是错的．
其中正确的有①④．（只填对应的序号）

20．函数y=$\sqrt{{x}^{2}-1}+\sqrt{1-{x}^{2}}+1$的定义域为A，值域为B，则A∩B=（　　）

以上都不对

1．已知函数f（x）=$\sqrt{x+1}+\frac{1}{x+2}$，则f（3）的值为（　　）