题目内容
如图, 为△
为△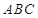 外接圆的切线,
外接圆的切线, 的延长线交直线
的延长线交直线 于点
于点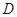 ,
,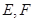 分别为弦
分别为弦 与弦
与弦 上的点,且
上的点,且 ,
,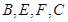 四点共圆.
四点共圆. 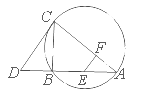
(Ⅰ)证明: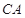 是△
是△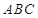 外接圆的直径;
外接圆的直径;
(Ⅱ)若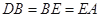 ,求过
,求过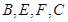 四点的圆的面积与△
四点的圆的面积与△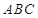 外接圆面积的比值.
外接圆面积的比值.
(I)见解析;(II)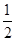 .
.
解析试题分析:(I)证明 是△
是△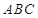 外接圆的直径,关键是证明
外接圆的直径,关键是证明 ,利用已知条件易于得到
,利用已知条件易于得到 ;在利用
;在利用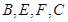 四点共圆,其对角互补即得证.
四点共圆,其对角互补即得证.
(II)通过连接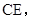 明确
明确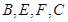 四点的圆的直径为
四点的圆的直径为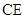 ,得到
,得到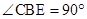 ;根据
;根据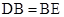 ,得
,得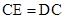 ,从而将圆面积之比,转化成
,从而将圆面积之比,转化成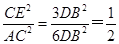 .
.
试题解析:(I)证明:∵ 为△
为△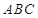 外接圆的切线,∴
外接圆的切线,∴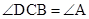 ,
,
∵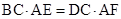 ,∴
,∴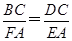 .
.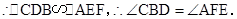
∵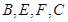 四点共圆,
四点共圆,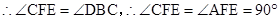 .
. 是△
是△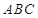 外接圆的直径;
外接圆的直径;
(II)连接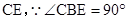 ,
,
∴过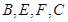 四点的圆的直径为
四点的圆的直径为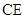 ,由
,由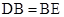 ,得
,得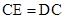 ,
,
又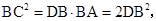
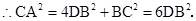
而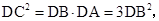
故过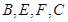 四点的圆的面积与△
四点的圆的面积与△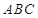 外接圆面积的比值为,
外接圆面积的比值为,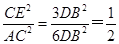 .
.
考点:与圆相关的比例线段

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

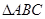 内接于
内接于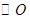 上,
上, ,
,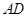 交
交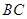 于点E,点F在DA的延长线上,
于点E,点F在DA的延长线上,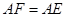 ,求证:
,求证: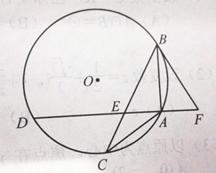
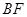 是
是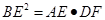 .
. 、
、 是圆
是圆 的半径,且
的半径,且 ,
, 是半径
是半径 交圆
交圆 ,过
,过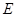 .求证:
.求证: .
.
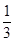 AC,AE=
AC,AE=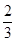 AB,BD,CE相交于点F.
AB,BD,CE相交于点F.
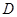 为
为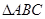 的
的 边上一点,
边上一点, 经过点
经过点 ,交
,交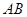 于另一点
于另一点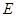 ,
, 经过点
经过点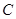 ,
, 于另一点
于另一点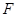 ,
, .
.
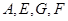 四点共圆;
四点共圆;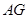 切
切 .
.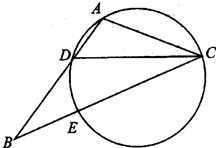
 是
是 的直径,弦
的直径,弦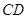 与
与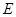 ,点
,点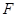 为弦
为弦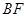 、
、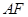 并延长交
并延长交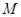 、
、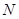 .
. 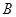 、
、 .
.
