题目内容
【题目】已知椭圆
的半焦距为
，左焦点为
，右顶点为
，抛物线
与椭圆交于
两点，若四边形
是菱形，则椭圆的离心率是( )
A. 
B. 
C. 
D. 
【答案】D
【解析】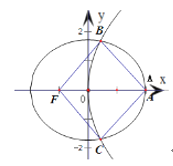
椭圆
的左焦点为
，右顶点为
，
抛物线
与椭圆交于
两点，
两点关于
轴对称，可设
四边形
是菱形，
，将
代入抛物线方程，得
，
，再代入椭圆方程，得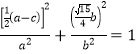
，化简整理，得
，解之得
不合题意，舍去），故答案为
.
【 方法点睛】本题主要考查抛物线的方程及椭圆的几何性质与离心率，属于难题.离心率的求解在圆锥曲线的考查中是一个重点也是难点，一般求离心率有以下几种情况：①直接求出
，从而求出
;②构造的齐次式，求出;③采用离心率的定义以及圆锥曲线的定义来求解;④根据圆锥曲线的统一定义求解．本题中，根据点在椭圆上可以建立关于焦半径和焦距的关系．从而找出之间的关系，求出离心率．
练习册系列答案
相关题目
