题目内容
(2012•黄浦区一模)已知函数y=f(x)是R上的偶函数,当x≥0时,有f(x)=
关于x的方程f(x)=m(m∈R)有且仅有四个不同的实数根,若α是四个根中的最大根,则sin(
+α)=
|
| π |
| 3 |
-
| 1 |
| 2 |
-
.| 1 |
| 2 |
分析:同一坐标系内作出函数y=f(x)的图象和直线y=m,因为两图象有且仅有四个公共点,所以m=1.再解方程f(x)=1,得最大根α=
,再代入再化简,即可得到sin(
+α)的值.
| 3π |
| 2 |
| π |
| 3 |
解答: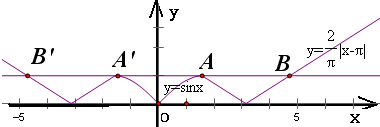 解:当x≥0时,函数在区间(0,
解:当x≥0时,函数在区间(0,
)和(π,+∞)上是增函数,在区间(
,π,)上是减函数
f(x)的极大值为f(
)=1,极小值为f(π)=0
作出函数当x≥0时的图象如右图
∵函数y=f(x)是R上的偶函数,
∴当x<0时y=f(x)的图象与当x≥0时的图象关于y轴对称,故函数x∈R时的图象如图所示
将直线y=m进行平移,可得当m=1时,两图象有且仅有四个不同的公共点,
相应地方程f(x)=m(m∈R)有且仅有四个不同的实数根.
令f(x)=1,得x1,2=±
,x3,4=±
,所以α=
,
∴sin(
+α)=sin(
+
)=sin
=-
故答案为:-
 解:当x≥0时,函数在区间(0,
解:当x≥0时,函数在区间(0,| π |
| 2 |
| π |
| 2 |
f(x)的极大值为f(
| π |
| 2 |
作出函数当x≥0时的图象如右图
∵函数y=f(x)是R上的偶函数,
∴当x<0时y=f(x)的图象与当x≥0时的图象关于y轴对称,故函数x∈R时的图象如图所示
将直线y=m进行平移,可得当m=1时,两图象有且仅有四个不同的公共点,
相应地方程f(x)=m(m∈R)有且仅有四个不同的实数根.
令f(x)=1,得x1,2=±
| π |
| 2 |
| 3π |
| 2 |
| 3π |
| 2 |
∴sin(
| π |
| 3 |
| π |
| 3 |
| 3π |
| 2 |
| 11π |
| 6 |
| 1 |
| 2 |
故答案为:-
| 1 |
| 2 |
点评:本题以分段函数为例,求方程的最大根和最小根,并且用这个根来求值,着重考查了函数与方程的关系,以及三角函数求值等知识,属于中档题.

练习册系列答案
相关题目
 (2012•黄浦区一模)已知四棱锥S-ABCD的底面ABCD是直角梯形,AB∥CD,BC⊥AB,侧面SAB为正三角形,AB=BC=4,CD=SD=2.如图所示.
(2012•黄浦区一模)已知四棱锥S-ABCD的底面ABCD是直角梯形,AB∥CD,BC⊥AB,侧面SAB为正三角形,AB=BC=4,CD=SD=2.如图所示.