题目内容
双曲线C与椭圆| x2 |
| 8 |
| y2 |
| 4 |
| 3 |
(1)求双曲线C的方程;
(2)过点P(0,4)的直线l,交双曲线C于A、B两点,交x轴于Q点(Q点与C的顶点不重合),当
| PQ |
| QA |
| QB |
| 8 |
| 3 |
分析:(1)先求出椭圆的焦点找到双曲线中的c,再利用直线y=
x为C的一条渐近线,求出a和b的关系进而求出双曲线C的方程;
(2)先把直线l的方程以及A、B两点的坐标设出来,利用
=λ1
=λ2
,找到λ1和λ2与A、B两点的坐标和直线l的斜率的关系,再利用A、B两点是直线和双曲线的交点以及λ1+λ2=-
,求出直线l的斜率k进而求出Q点的坐标.
| 3 |
(2)先把直线l的方程以及A、B两点的坐标设出来,利用
| PQ |
| QA |
| QB |
| 8 |
| 3 |
解答: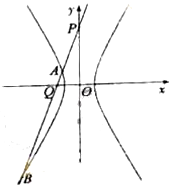 解:(Ⅰ)设双曲线方程为
解:(Ⅰ)设双曲线方程为
-
=1
由椭圆
+
=1
求得两焦点为(-2,0),(2,0),
∴对于双曲线C:c=2,又y=
x为双曲线C的一条渐近线
∴
=
解得a2=1,b2=3,
∴双曲线C的方程为x2-
=1
(Ⅱ)由题意知直线l得斜率k存在且不等于零,设l的方程:y=kx+4,A(x1,y1),B(x2,y2)
则Q(-
,0)
∵
=λ1
,
∴(-
,-4)=λ1(x1+
,y1).
∴λ1=
=-
同理λ2=-
,
所以λ1+λ2=-
-
=-
.
即2k2x1x2+5k(x1+x2)+8=0.(*)
又y=kx+4以及
x2-
=1
消去y得(3-k2)x2-8kx-19=0.
当3-k2=0时,则直线l与双曲线得渐近线平行,不合题意,3-k2≠0.
由韦达定理有:
x1+x2=
x1x2=-
代入(*)式得k2=4,k=±2
∴所求Q点的坐标为(±2,0).
 解:(Ⅰ)设双曲线方程为
解:(Ⅰ)设双曲线方程为| x2 |
| a2 |
| y2 |
| b2 |
由椭圆
| x2 |
| 8 |
| y2 |
| 4 |
求得两焦点为(-2,0),(2,0),
∴对于双曲线C:c=2,又y=
| 3 |
∴
| b |
| a |
| 3 |
∴双曲线C的方程为x2-
| y2 |
| 3 |
(Ⅱ)由题意知直线l得斜率k存在且不等于零,设l的方程:y=kx+4,A(x1,y1),B(x2,y2)
则Q(-
| 4 |
| k |
∵
| PQ |
| QA |
∴(-
| 4 |
| k |
| 4 |
| k |
∴λ1=
-
| ||
x1+
|
| 4 |
| kx1+4 |
同理λ2=-
| 4 |
| kx2+4 |
所以λ1+λ2=-
| 4 |
| kx1+4 |
| 4 |
| kx2+4 |
| 8 |
| 3 |
即2k2x1x2+5k(x1+x2)+8=0.(*)
又y=kx+4以及
x2-
| y2 |
| 3 |
消去y得(3-k2)x2-8kx-19=0.
当3-k2=0时,则直线l与双曲线得渐近线平行,不合题意,3-k2≠0.
由韦达定理有:
x1+x2=
| 8k |
| 3-k2 |
x1x2=-
| 19 |
| 3-k2 |
代入(*)式得k2=4,k=±2
∴所求Q点的坐标为(±2,0).
点评:本题综合考查了直线与双曲线的位置关系以及向量共线问题.在对圆锥曲线问题的考查上,一般都是出中等难度和高等难度的题.直线与圆锥曲线的位置关系,由于集中交汇了直线,圆锥曲线两章的知识内容,综合性强,能力要求高,还涉及到函数,方程,不等式,平面几何等许多知识,可以有效的考查函数与方程的思想,数形结合的思想,分类讨论的思想和转化化归的思想,因此,这一部分内容也成了高考的热点和重点.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目