题目内容
（本小题12分）设函数y=x
+ax
+bx+c的图像，如图所示，且与y=0在原点相切，若函数的极小值为–4，
（1）求a、b、c的值；
（2）求函数的递减区间。
【答案】
（1）-3 0 0
（2）函数的单调区间为（0,2）
【解析】解：（1）由图可知函数经过原点（0,0），代入函数得c=0-------------2分
导函数y
=3x
+2ax+b
-----------------------4分
函数图像在原点处与x轴相切，则（0,0）在其导函数图像上，代入得b=0 ------6分
则y= x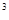
+ax y=3x+2ax，令y=3x+2ax=0，得x=0或x=－
a
由图可知－a>0
--------7分
|
x |
（－∞，0） |
0 |
（0，－ |
－ |
（－ |
|
f |
＋ |
0 |
－ |
0 |
＋ |
|
f(x) |
↗ |
极大值0 |
↘ |
极小值－ |
↗ |
可知极小值为－
+
，故－+=－4，解得a=－3 ------10分
（2）由（1）a=－3,得y=x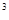－3x,－a=2
由上表显然函数的单调区间为（0,2）（或者表示为[0,2],区间开闭都行-----12分
练习册系列答案
开心蛙口算题卡系列答案
相关题目
的部分图象如图所示：
的值；
，当
时，求函数
的值域．
的图象恒过定点
，且点
的图象.
的值； （2）解不等式
；
有两个不等实根时，求
的取值范围.
是定义在
上的函数，对任意
，恒有
.
的值； ⑵求证：
且
，求
为常数，
满足
，则函数
的图象关于点
中心对称。”设函数
，定义域为A。
的图象关于点
中心对称；
时，求函数值
的取值范围；
，设计构造过程：
，若
，构造过程将继续下去；若
，构造过程都可以无限进行下去，求
的值。
的部分图象如图所示：
的值；
，当
时，求函数
的值域.
的部分图象如图所示：
的值；
，当
时，求函数
的值域．