题目内容
从1,2,3,…9这9个整数中任意取3个不同的数作为二次函数f(x)=ax2+bx+c的系数,则满足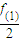 ∈Z的函数f(x)共有( )
∈Z的函数f(x)共有( )A.263个
B.264个
C.265个
D.266个
【答案】分析:由题意可得 f(1)=a+b+c是偶数,分①a,b,c里面三个都是偶数和②a,b,c里面一个偶数、两个奇数,两种情况,分别求得满足条件的(a,b,c)的个数,
相加即得所求.
解答:解:由题意可得 f(1)=a+b+c是偶数,若a,b,c里面三个都是偶数,则(a,b,c)共有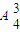 =24个.
=24个.
若a,b,c里面一个偶数,两个奇数,则(a,b,c)共有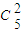 •
•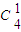 •
•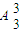 =10×4×6=240个.
=10×4×6=240个.
故满足满足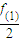 ∈Z的(a,b,c)一共有24+240=264 个,即满足
∈Z的(a,b,c)一共有24+240=264 个,即满足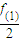 ∈Z的函数f(x)共有24个,
∈Z的函数f(x)共有24个,
故选B.
点评:本题主要考查二次函数的性质,排列组合的应用,体现了转化的数学思想,属于基础题.
相加即得所求.
解答:解:由题意可得 f(1)=a+b+c是偶数,若a,b,c里面三个都是偶数,则(a,b,c)共有
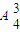 =24个.
=24个.若a,b,c里面一个偶数,两个奇数,则(a,b,c)共有
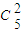 •
•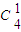 •
•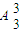 =10×4×6=240个.
=10×4×6=240个.故满足满足
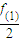 ∈Z的(a,b,c)一共有24+240=264 个,即满足
∈Z的(a,b,c)一共有24+240=264 个,即满足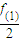 ∈Z的函数f(x)共有24个,
∈Z的函数f(x)共有24个,故选B.
点评:本题主要考查二次函数的性质,排列组合的应用,体现了转化的数学思想,属于基础题.

练习册系列答案
相关题目
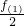 ∈Z的函数f(x)共有
∈Z的函数f(x)共有