题目内容
从1,2,3,…9这9个整数中任意取3个不同的数作为二次函数f(x)=ax2+bx+c的系数,则满足
∈Z的函数f(x)共有( )
| f(1) |
| 2 |
| A.263个 | B.264个 | C.265个 | D.266个 |
由题意可得 f(1)=a+b+c是偶数,若a,b,c里面三个都是偶数,则(a,b,c)共有
=24个.
若a,b,c里面一个偶数,两个奇数,则(a,b,c)共有
•
•
=10×4×6=240个.
故满足满足
∈Z的(a,b,c)一共有24+240=264 个,即满足
∈Z的函数f(x)共有24个,
故选B.
| A | 34 |
若a,b,c里面一个偶数,两个奇数,则(a,b,c)共有
| C | 25 |
| C | 14 |
| A | 33 |
故满足满足
| f(1) |
| 2 |
| f(1) |
| 2 |
故选B.

练习册系列答案
相关题目
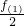 ∈Z的函数f(x)共有
∈Z的函数f(x)共有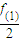 ∈Z的函数f(x)共有( )
∈Z的函数f(x)共有( )