题目内容
已知四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=2EC.
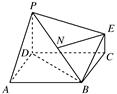
(1)求证:BE∥平面PDA;
(2)若N为线段PB的中点,求证:NE⊥平面PDB.

(1)求证:BE∥平面PDA;
(2)若N为线段PB的中点,求证:NE⊥平面PDB.
(1)见解析(2)见解析
(1)∵EC∥PD,PD?平面PDA,EC?平面PDA,
∴EC∥平面PDA,
同理可得BC∥平面PDA.
∵EC?平面EBC,BC?平面BEC且EC∩BC=C,
∴平面BEC∥平面PDA.
又∵BE?平面BEC,∴BE∥平面PDA.
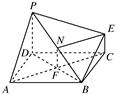
(2)连接AC,交BD于点F,连接NF,
∵F为BD的中点,
∴NF∥PD且NF= PD,
PD,
又EC∥PD且EC= PD,
PD,
∴NF∥EC且NF=EC.
∴四边形NFCE为平行四边形,
∴NE∥FC,
∵PD⊥平面ABCD,AC?平面ABCD,∴AC⊥PD,
又DB⊥AC,PD∩BD=D,∴AC⊥平面PDB,
∴NE⊥平面PDB.
∴EC∥平面PDA,
同理可得BC∥平面PDA.
∵EC?平面EBC,BC?平面BEC且EC∩BC=C,
∴平面BEC∥平面PDA.
又∵BE?平面BEC,∴BE∥平面PDA.

(2)连接AC,交BD于点F,连接NF,
∵F为BD的中点,
∴NF∥PD且NF=
 PD,
PD,又EC∥PD且EC=
 PD,
PD,∴NF∥EC且NF=EC.
∴四边形NFCE为平行四边形,
∴NE∥FC,
∵PD⊥平面ABCD,AC?平面ABCD,∴AC⊥PD,
又DB⊥AC,PD∩BD=D,∴AC⊥平面PDB,
∴NE⊥平面PDB.

练习册系列答案
相关题目
 中,
中, 平面
平面 ,底面
,底面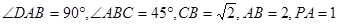 .
.
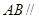 平面
平面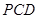 ;
;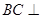 平面
平面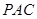 ;
;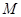 是
是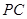 的中点,求三棱锥
的中点,求三棱锥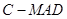 的体积.
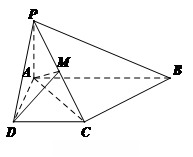
的体积.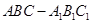 中,D、E分别是BC和
中,D、E分别是BC和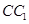 的中点,已知AB=AC=AA1=4,ÐBAC=90°.
的中点,已知AB=AC=AA1=4,ÐBAC=90°.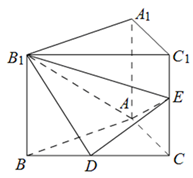
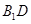 ⊥平面
⊥平面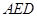 ;
;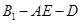 的余弦值;
的余弦值;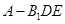 的体积.
的体积.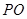 中,已知
中,已知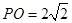 ,
,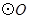 的直径
的直径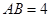 ,点
,点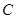 在底面圆周上,且
在底面圆周上,且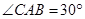 ,
,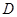 为
为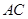 的中点.
的中点.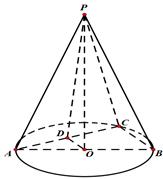
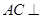 平面
平面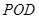 ;
;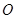 到面
到面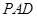 的距离.
的距离.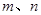 是不同的直线,
是不同的直线,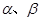 是不同的平面,有以下四个命题:
是不同的平面,有以下四个命题: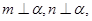 则
则
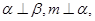 则
则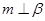
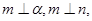 则
则
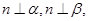 则
则
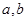 和平面
和平面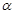 ,且
,且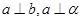 ,则
,则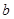 与
与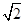 .
.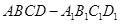 中,点
中,点 是棱
是棱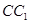 上的一个动点,平面
上的一个动点,平面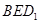 交棱
交棱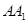 于点
于点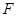 .则下列命题中假命题是( )
.则下列命题中假命题是( )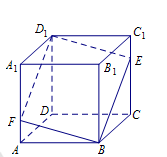
 //平面
//平面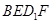
 平面
平面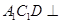 平面
平面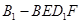 的体积均不变
的体积均不变