题目内容
已知条件p:(x+1)2>4,条件q:x>a,且q是p的充分而不必要条件,则a的取值范围是( )
| A、a≥1 | B、a≤1? | C、a≥-3? | D、a≤-3? |
分析:先求出p,q的等价条件,利用q是p的充分而不必要条件,建立条件关系即可求a的取值范围
解答:解:由:(x+1)2>4,得x+1>2或x+1<-2,即x>1或x<-3,即p:x>1或x<-3,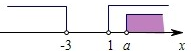
∵q是p的充分而不必要条件,
∴q⇒p,但q⇒p不成立,
则a≥1,
故选:A.

∵q是p的充分而不必要条件,
∴q⇒p,但q⇒p不成立,
则a≥1,
故选:A.
点评:本题主要考查充分条件和必要条件的应用,利用不等式的性质求出p,利用数形结合是解决本题的关键.

练习册系列答案
相关题目