题目内容
已知函数f(x)=x2+bx+c(b,c∈R)为偶函数,如果点A(x,y)在函数f(x)的图象上,且点B(x,y2+1)在g(x)=f(x2+c)的图象上.(1)求函数f(x)的解析式;
(2)设F(x)=g(x)-λf(x).是否存在实数λ,使F(x)在
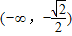 上为减函数,且在
上为减函数,且在 上为增函数?若存在,求出λ的值;若不存在,请说明理由.
上为增函数?若存在,求出λ的值;若不存在,请说明理由.
【答案】分析:利用偶函数的定义列出恒成立的等式,求出b的值;再点A(x,y)在函数f(x)的图象上,且点B(x,y2+1)在g(x)=f(x2+c)的图象上,求出b,c的值;
(2)由f(x)求g(x),再求F(x)解析式,求F(x1)-F(x2)的表达式,最后要变形为因式相乘的形式;根据单调性得出这个式子的正负,从而得出λ的范围,由两个范围取交集可得λ的值.
解答:解:(1)∵f(x)=x2+bx+c为偶函数,故f(-x)=f(x),即有(-x)2+b(-x)+c=x2+bx+c,解得b=0.
由因为点A(x,y)在函数f(x)的图象上,且点B(x,y2+1)在g(x)=f(x2+c)的图象上,所以c=1,所以f(x)=x2+1
(2)解:g(x)=f(x2+1)=(x2+1)2+1=x4+2x2+2.
F(x)=g(x)-λf(x)=x4+(2-λ)x2+(2-λ),F(x1)-F(x2)=(x1+x2)(x1-x2)[x12+x22+(2-λ)]
由题设当x1<x2< 时,(x1+x2)(x1-x2)>0,x12+x22+(2-λ)>
时,(x1+x2)(x1-x2)>0,x12+x22+(2-λ)> +
+ +2-λ=3-λ,
+2-λ=3-λ,
则3-λ≥0,λ≤3;
当 <x1<x2<0时,(x1+x2)(x1-x2)>0,x12+x22+(2-λ)>
<x1<x2<0时,(x1+x2)(x1-x2)>0,x12+x22+(2-λ)> +
+ +2-λ=3-λ,
+2-λ=3-λ,
则3-λ≥0,λ≥3故λ=3.
点评:解决函数的奇偶性问题,一般利用奇函数、偶函数的定义找关系;注意具有奇偶性的函数的定义域关于原点对称;求参数的值,用函数的单调性定义求解,属于定义的逆用,知单调性来判断差的正负.
(2)由f(x)求g(x),再求F(x)解析式,求F(x1)-F(x2)的表达式,最后要变形为因式相乘的形式;根据单调性得出这个式子的正负,从而得出λ的范围,由两个范围取交集可得λ的值.
解答:解:(1)∵f(x)=x2+bx+c为偶函数,故f(-x)=f(x),即有(-x)2+b(-x)+c=x2+bx+c,解得b=0.
由因为点A(x,y)在函数f(x)的图象上,且点B(x,y2+1)在g(x)=f(x2+c)的图象上,所以c=1,所以f(x)=x2+1
(2)解:g(x)=f(x2+1)=(x2+1)2+1=x4+2x2+2.
F(x)=g(x)-λf(x)=x4+(2-λ)x2+(2-λ),F(x1)-F(x2)=(x1+x2)(x1-x2)[x12+x22+(2-λ)]
由题设当x1<x2<
 时,(x1+x2)(x1-x2)>0,x12+x22+(2-λ)>
时,(x1+x2)(x1-x2)>0,x12+x22+(2-λ)> +
+ +2-λ=3-λ,
+2-λ=3-λ,则3-λ≥0,λ≤3;
当
 <x1<x2<0时,(x1+x2)(x1-x2)>0,x12+x22+(2-λ)>
<x1<x2<0时,(x1+x2)(x1-x2)>0,x12+x22+(2-λ)> +
+ +2-λ=3-λ,
+2-λ=3-λ,则3-λ≥0,λ≥3故λ=3.
点评:解决函数的奇偶性问题,一般利用奇函数、偶函数的定义找关系;注意具有奇偶性的函数的定义域关于原点对称;求参数的值,用函数的单调性定义求解,属于定义的逆用,知单调性来判断差的正负.

练习册系列答案
相关题目
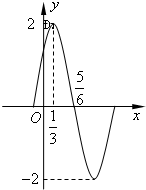 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|