题目内容
若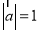 ,
,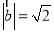 ,
,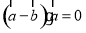 ,则
,则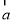 与
与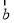 的夹角为 .
的夹角为 .
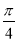
【解析】
试题分析:设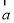 与
与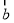 的夹角为
的夹角为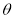 ,则
,则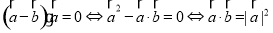
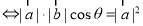 ,而
,而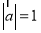 ,
,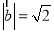 ,所以
,所以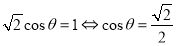 ,而
,而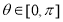 ,故
,故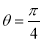 .
.
考点:平面向量的数量积.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
题目内容
若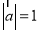 ,
,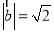 ,
,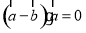 ,则
,则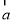 与
与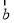 的夹角为 .
的夹角为 .
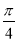
【解析】
试题分析:设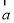 与
与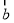 的夹角为
的夹角为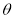 ,则
,则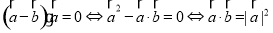
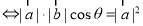 ,而
,而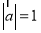 ,
,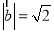 ,所以
,所以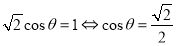 ,而
,而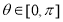 ,故
,故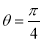 .
.
考点:平面向量的数量积.

 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案