题目内容
【题目】已知函数f(x)的定义域为实数集R,及整数k、T;
(1)若函数f(x)=2xsin(πx),证明f(x+2)=4f(x);
(2)若f(x+T)=kf(x),且f(x)=axφ(x)(其中a为正的常数),试证明:函数φ(x)为周期函数;
(3)若f(x+6)= ![]() f(x),且当x∈[﹣3,3]时,f(x)=
f(x),且当x∈[﹣3,3]时,f(x)= ![]() (x2﹣9),记Sn=f(2)+f(6)+f(10)+…+f(4n﹣2),n∈N+ , 求使得S1、S2、S3、…、Sn小于1000都成立的最大整数n.
(x2﹣9),记Sn=f(2)+f(6)+f(10)+…+f(4n﹣2),n∈N+ , 求使得S1、S2、S3、…、Sn小于1000都成立的最大整数n.
【答案】
(1)证明:f(x+2)=2x+2sin(π(x+2))=4×2xsin(πx)=4f(x),
∴f(x+2)=4f(x).
(2)证明:设k=aT,a=k﹣T.而φ(x)=a﹣xf(x),
∴φ(x+T)=a﹣x﹣Tf(x+T)=a﹣x﹣TaTf(x)=a﹣xf(x)=φ(x),
∴φ(x)是以T为周期的周期函数
(3)解:取n=3k(k∈N*),令Sn=Rk.则Rk=f(2)+f(6)+f(10)+…+f(2k﹣10)+f(12k﹣6)+f(12k﹣2),
又f(0)=0.而f(x+6)= ![]() f(x),
f(x),
∴f(6k)=0,又Rk=f(2)+f(10)+…+f(2k﹣10)+f(12k﹣2),
而f(2)=﹣1,f(10)= ![]() f(4)=2f(﹣2)=2.
f(4)=2f(﹣2)=2.
又f(12(k+1)﹣10)+f(12(k+1)﹣2)=2[f(12k﹣10)+f(12k﹣2)],
∴数列{f(12k﹣10)+f(12k﹣2)}是以f(2)+f(10)=1为首项,2为公比的等比数列,
∴Rk=2k﹣1,
由Rk<1000,解得9<k<10,即n=28,29.
当n=28时,f(110)<0;n=29时,f(114)=0.
∴满足条件的最大正整数n=29
【解析】(1)代入计算即可证明.(2)设k=aT , a=k﹣T . 而φ(x)=a﹣xf(x),可得φ(x+T)=φ(x),即可证明.(3)取n=3k(k∈N*),令Sn=Rk . 则Rk=f(2)+f(6)+f(10)+…+f(2k﹣10)+f(12k﹣6)+f(12k﹣2),又f(0)=0.而f(x+6)= ![]() f(x),可得f(6k)=0,而f(2)=﹣1,f(10)=2.可得:f(12(k+1)﹣10)+f(12(k+1)﹣2)=2[f(12k﹣10)+f(12k﹣2)],利用等比数列的前n项和公式即可得出.
f(x),可得f(6k)=0,而f(2)=﹣1,f(10)=2.可得:f(12(k+1)﹣10)+f(12(k+1)﹣2)=2[f(12k﹣10)+f(12k﹣2)],利用等比数列的前n项和公式即可得出.
【考点精析】根据题目的已知条件,利用数列的前n项和的相关知识可以得到问题的答案,需要掌握数列{an}的前n项和sn与通项an的关系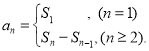 .
.

 53随堂测系列答案
53随堂测系列答案