题目内容
在等差数列{an}中,a1+a3=8,且a4为a2和a9的等比中项,求数列{an}的首项、公差及前n项和.
设该数列的公差为d,前n项和为Sn.由已知可得
2a1+2d=8,(a1+3d)2=(a1+d)(a1+8d),
所以a1+d=4,d(d-3a1)=0,
解得a1=4,d=0或a1=1,d=3,即数列{an}的首项为4,公差为0,或首项为1,公差为3.
所以数列的前n项和Sn=4n或Sn= .
.
2a1+2d=8,(a1+3d)2=(a1+d)(a1+8d),
所以a1+d=4,d(d-3a1)=0,
解得a1=4,d=0或a1=1,d=3,即数列{an}的首项为4,公差为0,或首项为1,公差为3.
所以数列的前n项和Sn=4n或Sn=
 .
.
练习册系列答案
相关题目
 的前n项和是Sn,若
的前n项和是Sn,若 都是等差数列,且公差相等,则数列
都是等差数列,且公差相等,则数列



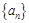 中,
中,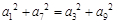 ,记
,记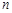 项和为
项和为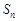 ,其中
,其中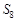
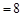 ,则
,则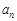 = .
= .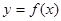 的图像如下列图中,经过原点和(1,1),且对任意
的图像如下列图中,经过原点和(1,1),且对任意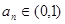 ,由关系式
,由关系式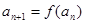 得到数列{
得到数列{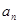 },满足
},满足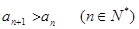 ,则该函数的图像为( )
,则该函数的图像为( )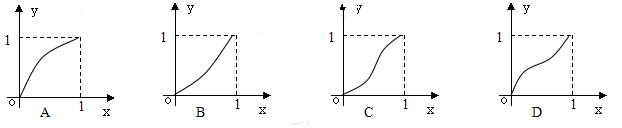
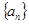 的前
的前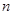 项和
项和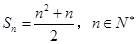 .
.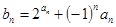 ,求数列
,求数列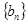 的前
的前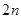 项和.
项和.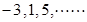 的第15项为( )
的第15项为( ) 中,
中,
 ,则此数列前30项和等于( )
,则此数列前30项和等于( )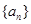 中,
中,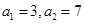 ,当
,当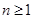 时,
时,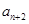 等于
等于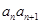 的个位数,则该数列的第2014项是
的个位数,则该数列的第2014项是