题目内容
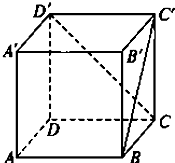 如图所示,已知正方体ABCD-A′B′C′D′,求:
如图所示,已知正方体ABCD-A′B′C′D′,求:(1)BC′与CD′所成的角;
(2)AD与BC′所成的角.
分析:(1)连结BA'、A'C',利用正方体的性质得到四边形A'D'CB是平行四边形,得BA'∥CD',从而∠A'BC'就是BC'与CD'所成的角.正三角形△A'BC'求得∠A'BC'=60°,即得BC'与CD'所成的角的大小;
(2)由AD∥BC,可得∠C'BC就是异面直线AD与BC′所成的角.等腰Rt△BB'C'中,算出∠C'BC=45°,即得AD与BC′所成的角.
(2)由AD∥BC,可得∠C'BC就是异面直线AD与BC′所成的角.等腰Rt△BB'C'中,算出∠C'BC=45°,即得AD与BC′所成的角.
解答:解:(1)连结BA'、A'C',则
∵正方体ABCD-A'B'C'D'中,A'D'∥BC,A'D'=BC.
∴四边形A'D'CB是平行四边形,可得BA'∥CD',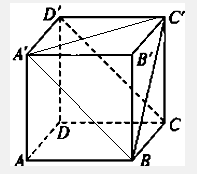
则∠A'BC'就是BC'与CD'所成的角.
∵△A'BC'为正三角形,可得∠A'BC'=60°.
即BC'与CD'所成的角为60°.…(6分)
(2)由正方体ABCD-A'B'C'D'中,可得AD∥BC,
∴∠C'BC就是异面直线AD与BC′所成的角.
∵Rt△BB'C'中,BB'=B'C'
∴∠C'BC=45°,即AD与BC′所成的角等于45°.…(12分)
∵正方体ABCD-A'B'C'D'中,A'D'∥BC,A'D'=BC.
∴四边形A'D'CB是平行四边形,可得BA'∥CD',

则∠A'BC'就是BC'与CD'所成的角.
∵△A'BC'为正三角形,可得∠A'BC'=60°.
即BC'与CD'所成的角为60°.…(6分)
(2)由正方体ABCD-A'B'C'D'中,可得AD∥BC,
∴∠C'BC就是异面直线AD与BC′所成的角.
∵Rt△BB'C'中,BB'=B'C'
∴∠C'BC=45°,即AD与BC′所成的角等于45°.…(12分)
点评:本题在正方体中求异面直线所成角的大小.着重考查了正方体的性质、异面直线所成角定义与求法等知识,属于中档题.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
 如图所示,已知正方体ABCD-A1B1C1D1的棱长为a,E,F分别是BC,A1D1的中点.
如图所示,已知正方体ABCD-A1B1C1D1的棱长为a,E,F分别是BC,A1D1的中点.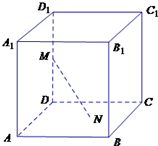 如图所示,已知正方体ABCD-A1B1C1D1的棱长为2,长为2的线段MN的一个端点M在棱DD1上运动,另一端点N在正方形ABCD内运动,则MN的中点的轨迹的面积为( )
如图所示,已知正方体ABCD-A1B1C1D1的棱长为2,长为2的线段MN的一个端点M在棱DD1上运动,另一端点N在正方形ABCD内运动,则MN的中点的轨迹的面积为( )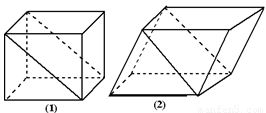
 的概率P1;
的概率P1; 的概率P2。
的概率P2。