题目内容
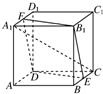 如图所示,已知正方体ABCD-A1B1C1D1的棱长为a,E,F分别是BC,A1D1的中点.
如图所示,已知正方体ABCD-A1B1C1D1的棱长为a,E,F分别是BC,A1D1的中点.(1)求证:四边形B1EDF为菱形;
(2)求A1C与DE所成的角的余弦值.
分析:(1)要证四边形B1EDF为菱形,只要先证其是平行四边形,再说明邻边相等即可,根据正方体的性质易证;
(2)根据异面直线所成角的定义,把直线A1C平移和直线DE相交,找到异面直线A1C与DE所成的角,解三角形即可求得结果.
(2)根据异面直线所成角的定义,把直线A1C平移和直线DE相交,找到异面直线A1C与DE所成的角,解三角形即可求得结果.
解答: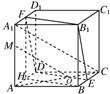 解:(1)证明:取AD中点H,连接BH,FH,
解:(1)证明:取AD中点H,连接BH,FH,
易证:FHBB1为矩形,
因此,FB1∥BH,且FB1=BH,.
又∵正方形ABCD中BH∥DE且BH=DE,
∴FB1∥DE,FB1=DE,
∴FB1ED为平行四边形.
又∵FD=DE=
=
a,
∴四边形B1EDF为菱形.
(2)连接AC交DE于点O,
则
=
=
=
.
过O点作OM∥A1C交AA1于点M,
则∠MOD或其补角为DE与A1C所成的角.
在△MOD中,OD=
DE=
×
a=
a,
MO=
A1C=
×
a=
a,
MD=
=
a,
cos∠MOD=
.
∴A1C与DE所成的角的余弦值等于
.
 解:(1)证明:取AD中点H,连接BH,FH,
解:(1)证明:取AD中点H,连接BH,FH,易证:FHBB1为矩形,
因此,FB1∥BH,且FB1=BH,.
又∵正方形ABCD中BH∥DE且BH=DE,
∴FB1∥DE,FB1=DE,
∴FB1ED为平行四边形.
又∵FD=DE=
a2+(
|
| ||
| 2 |
∴四边形B1EDF为菱形.
(2)连接AC交DE于点O,
则
| AO |
| OC |
| DO |
| OE |
| AD |
| EC |
| 2 |
| 1 |
过O点作OM∥A1C交AA1于点M,
则∠MOD或其补角为DE与A1C所成的角.
在△MOD中,OD=
| 2 |
| 3 |
| 2 |
| 3 |
| ||
| 2 |
| ||
| 3 |
MO=
| 2 |
| 3 |
| 2 |
| 3 |
| 3 |
2
| ||
| 3 |
MD=
(
|
| ||
| 3 |
cos∠MOD=
| ||
| 15 |
∴A1C与DE所成的角的余弦值等于
| ||
| 15 |
点评:此题是个中档题.考查异面直线所成的角和棱柱的结构特征,以及解决异面直线所成的角的方法(平移法)的应用,体现了转化的思想和数形结合的思想方法.

练习册系列答案
相关题目
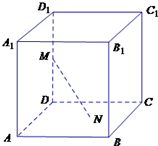 如图所示,已知正方体ABCD-A1B1C1D1的棱长为2,长为2的线段MN的一个端点M在棱DD1上运动,另一端点N在正方形ABCD内运动,则MN的中点的轨迹的面积为( )
如图所示,已知正方体ABCD-A1B1C1D1的棱长为2,长为2的线段MN的一个端点M在棱DD1上运动,另一端点N在正方形ABCD内运动,则MN的中点的轨迹的面积为( )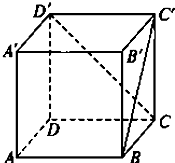 如图所示,已知正方体ABCD-A′B′C′D′,求:
如图所示,已知正方体ABCD-A′B′C′D′,求: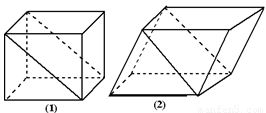
 的概率P1;
的概率P1; 的概率P2。
的概率P2。