题目内容
20.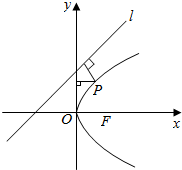 已知直线l1:4x-3y+6=0和直线l2:x=0,抛物线y2=4x上一动点P到直线l1和直线l2的距离之和的最小值是( )
已知直线l1:4x-3y+6=0和直线l2:x=0,抛物线y2=4x上一动点P到直线l1和直线l2的距离之和的最小值是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 抛物线y2=4x上一动点P到直线l1和直线l2的距离之和转化为:抛物线y2=4x上一动点P到直线l1和直线x=1的距离之和,x=-1是抛物线y2=4x的准线,则P到x=-1的距离等于PF,抛物线y2=4x的焦点F(1,0)过P作4x-3y+6=0垂线,和抛物线的交点就是P,所以点P到直线l1:4x-3y+6=0的距离和到直线l2:x=-1的距离之和的最小值就是F(1,0)到直线4x-3y+6=0距离.
解答 解:x=-1是抛物线y2=4x的准线,则P到x=-1的距离等于PF,
抛物线y2=4x的焦点F(1,0)
过P作4x-3y+6=0垂线,和抛物线的交点就是P,
所以点P到直线l1:4x-3y+6=0的距离和到直线l2:x=-1的距离之和的最小值
就是F(1,0)到直线4x-3y+6=0距离,
所以最小值=$\frac{|4-0+6|}{\sqrt{{4}^{2}+{(-3)}^{2}}}$=2.
直线l1:4x-3y+6=0和直线l2:x=0,抛物线y2=4x上一动点P到直线l1和直线l2的距离之和的最小值是:2-1=1
故选:A.
点评 本题考查点到直线的距离公式的求法,是中档题.解题时要认真审题,注意抛物线的性质的灵活运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.若点(16,tanθ)在函数y=log2x的图象上,则$\frac{1+cos2θ+8si{n}^{2}θ}{sin2θ}$=( )
| A. | $\frac{20\sqrt{3}}{3}$ | B. | $\frac{65}{4}$ | C. | 4 | D. | 4$\sqrt{2}$ |
15.函数f(x)=x5+x3+x的图象( )
| A. | 关于y轴对称 | B. | 关于直线y=x对称 | ||
| C. | 关于坐标原点对称 | D. | 关于直线y=-x对称 |
10.在复平面内,复数z=$\frac{i-2}{i}$的对应点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
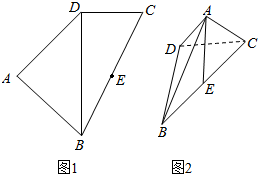 如图,四边形ABCD中(图1),E是BC的中点,DB=2,DC=1,BC=$\sqrt{5}$,AB=AD=$\sqrt{2}$,将(图1)沿直线BD折起,使二面角A-BD-C成锐二面角且三棱锥A-BDC的体积为$\frac{\sqrt{3}}{6}$.(如图2)
如图,四边形ABCD中(图1),E是BC的中点,DB=2,DC=1,BC=$\sqrt{5}$,AB=AD=$\sqrt{2}$,将(图1)沿直线BD折起,使二面角A-BD-C成锐二面角且三棱锥A-BDC的体积为$\frac{\sqrt{3}}{6}$.(如图2)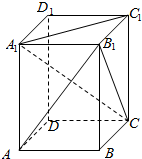 如图,在正四棱柱ABCD-A1B1C1D1中,∠B1AB=60°
如图,在正四棱柱ABCD-A1B1C1D1中,∠B1AB=60°